Введение в квантование LLM. Уменьшение размера больших языковых моделей с помощью 8-битного квантования
Крупные языковые модели (Large Language Models, LLMs) известны своими значительными вычислительными требованиями. Обычно размер модели рассчитывается путём умножения количества параметров (размера) на точность их представления (тип данных). Однако для экономии памяти веса модели могут храниться с использованием типов данных с меньшей разрядностью благодаря процессу, известному как квантизация.
В литературе выделяют две основные группы методов квантизации весов:
- Пост-тренировочная квантизация (Post-Training Quantization, PTQ) — это простой метод, при котором веса уже обученной модели преобразуются в формат с меньшей разрядностью без необходимости повторного обучения. Хотя PTQ легко реализовать, она может приводить к потенциальному снижению производительности модели.
- Квантизация с учётом обучения (Quantization-Aware Training, QAT) включает процесс преобразования весов на этапе предобучения или тонкой настройки (SFT), что позволяет улучшить качество модели. Однако QAT требует значительных вычислительных ресурсов и наличия репрезентативных обучающих данных.
В данной статье мы сосредоточимся на PTQ для снижения разрядности параметров. Чтобы лучше понять процесс, мы применим как наивные, так и более продвинутые методы квантизации на примере модели GPT-2.
Предпосылки: представление чисел с плавающей запятой
Выбор типа данных определяет объём необходимых вычислительных ресурсов, влияя на скорость и эффективность модели. В задачах глубокого обучения баланс между точностью и вычислительной качеством становится критически важным, так как высокая точность часто требует больших вычислительных затрат.
Среди различных типов данных в глубоком обучении преимущественно используются числа с плавающей запятой благодаря их способности представлять широкий диапазон значений с высокой точностью. Обычно число с плавающей запятой использует n бит для хранения числового значения, которые делятся на три компонента:
- Знак (Sign): Один бит указывает на положительное или отрицательное значение числа. 0 обозначает положительное число, 1 — отрицательное.
- Экспонента (Exponent): Группа бит, представляющая степень, в которую возводится основание (обычно 2 в двоичной системе). Экспонента может быть как положительной, так и отрицательной, что позволяет представлять очень большие или очень малые значения.
- Мантисса (Significand/Mantissa): Оставшиеся биты хранят мантиссу — значимые цифры числа. Точность числа сильно зависит от длины мантиссы.
Такая структура позволяет числам с плавающей запятой охватывать широкий диапазон значений с разной степенью точности. Формула для представления числа с плавающей запятой выглядит следующим образом: (Нажмите Enter или кликните, чтобы увидеть изображение в полном размере)
Наиболее распространённые типы данных в глубоком обучении
Рассмотрим три ключевых формата:
- FP32 (float32): Использует 32 бита: 1 бит на знак, 8 бит на экспоненту и 23 бита на мантиссу. Обеспечивает высокую точность, но требует значительных вычислительных и память-затрат.
- FP16 (float16): Использует 16 бит: 1 бит на знак, 5 бит на экспоненту и 10 бит на мантиссу. Более экономичен по памяти и ускоряет вычисления, но сниженная разрядность и диапазон могут приводить к числовой нестабильности, что влияет на точность модели.
- BF16 (bfloat16): Также 16-битный формат, но с распределением: 1 бит на знак, 8 бит на экспоненту и 7 бит на мантиссу. BF16 расширяет диапазон представимых значений по сравнению с FP16, снижая риски переполнения и исчезновения порядка. Несмотря на меньшую точность из-за сокращённой мантиссы, BF16 обычно незначительно влияет на качество модели и является полезным компромиссом для задач глубокого обучения.
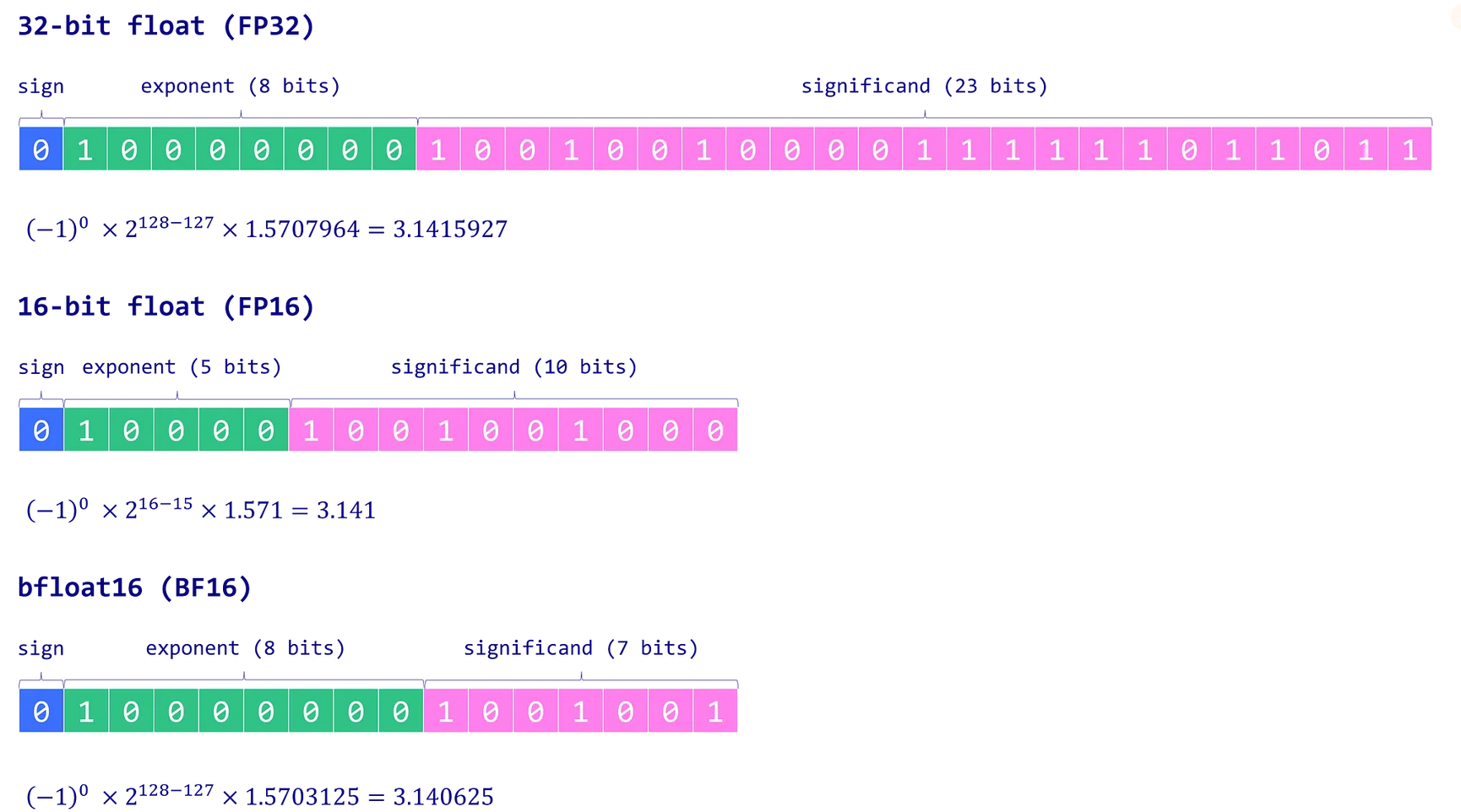
Рис. 1. Основные числовые типы весов
В терминологии машинного обучения FP32 часто называют "полной точностью" (4 байта), тогда как BF16 и FP16 относят к "половинной точности" (2 байта). Но можно ли пойти ещё дальше и хранить веса, используя всего один байт? Ответ — тип данных INT8, который представляет собой 8-битное значение и способен хранить 2⁸ = 256 различных значений. В следующем разделе мы рассмотрим, как преобразовать веса из формата FP32 в INT8.
Наивная 8-битная квантизация
В этом разделе мы реализуем две техники квантизации: симметричную (с использованием абсолютного максимума, absmax) и асимметричную (с использованием zero-point квантизации). В обоих случаях цель состоит в том, чтобы преобразовать тензор FP32 (исходные веса) в тензор INT8 (квантизованные веса).
При absmax-квантизации исходное число делится на абсолютное максимальное значение тензора и умножается на масштабирующий коэффициент (127), чтобы отобразить значения в диапазон [-127, 127]. Для восстановления исходных значений FP16 квантизованное число INT8 делится на коэффициент квантизации, при этом неизбежно теряется часть точности из-за округления.
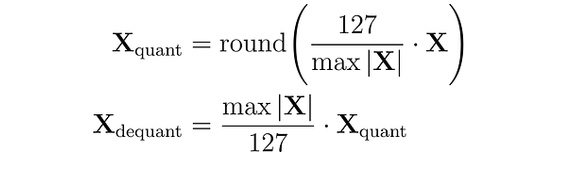
Рис. 2. Схема симметричного кванотования в 8 бит
Например, предположим, что абсолютное максимальное значение равно 3.2. Тогда вес 0.1 будет квантизован как round(0.1 × 127/3.2) = 4. Если мы захотим деквантизовать его, то получим 4 × 3.2/127 = 0.1008, что означает ошибку в 0.008.
Вот соответствующая реализация на Python:
import torch
def absmax_quantize(X):
# Вычисляем масштаб
scale = 127 / torch.max(torch.abs(X))
# Квантизуем
X_quant = (scale * X).round()
# Деквантизуем
X_dequant = X_quant / scale
return X_quant.to(torch.int8), X_dequantПри квантизации с нулевой точкой (zero-point quantization) можно учитывать асимметричные распределения входных данных, что полезно, например, для выходов функции ReLU (только положительные значения). Сначала входные значения масштабируются на основе полного диапазона значений (255), делённого на разницу между максимальным и минимальным значениями. Затем это распределение сдвигается на нулевую точку, чтобы отобразить его в диапазон [-128, 127] (обратите внимание на дополнительное значение по сравнению с absmax). Сначала вычисляются масштабный коэффициент и нулевая точка:
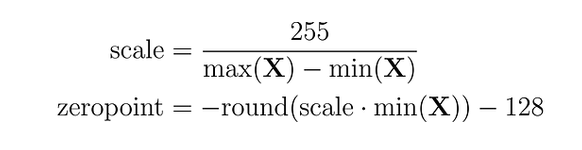
Рис. 3. Коэффициенты асимметричного кванотования в 8 бит
Затем эти переменные используются для квантизации или деквантизации весов:
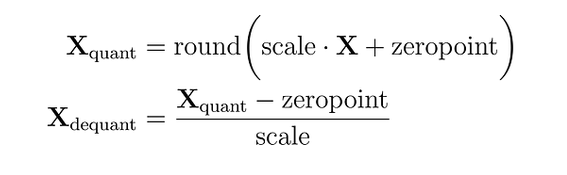
Рис. 4. Схема асимметричного кванотования в 8 бит
Рассмотрим пример: максимальное значение равно 3.2, минимальное — -3.0. Масштаб будет равен 255/(3.2 + 3.0) = 41.13, а нулевая точка: -round(41.13 × -3.0) - 128 = 123 - 128 = -5. Таким образом, наш предыдущий вес 0.1 будет квантизован как round(41.13 × 0.1 - 5) = -1. Это сильно отличается от значения, полученного с помощью absmax (4 против -1).
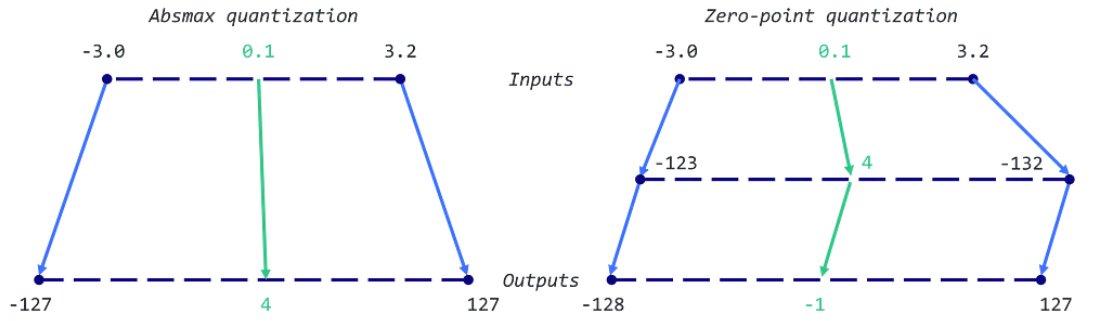
Рис. 5. Сравнение схем квантования симметричного и асимметричного
Реализация на Python довольно проста:
def zeropoint_quantize(X):
# Вычисляем диапазон значений (знаменатель)
x_range = torch.max(X) - torch.min(X)
x_range = 1 if x_range == 0 else x_range
# Вычисляем масштаб
scale = 255 / x_range
# Сдвигаем на нулевую точку
zeropoint = (-scale * torch.min(X) - 128).round()
# Масштабируем и округляем входные данные
X_quant = torch.clip((X * scale + zeropoint).round(), -128, 127)
# Деквантизуем
X_dequant = (X_quant - zeropoint) / scale
return X_quant.to(torch.int8), X_dequantВместо того чтобы рассматривать игрушечные примеры, мы можем попробовать квантихацию на примере реальной модели в экосистеме библиотеки transformers.
Начнём с загрузки модели и токенизатора для GPT-2. Это очень маленькая модель, которую, конечно, не стоит квантизовать, но она подойдёт для этого примера. Сначала мы хотим оценить размер модели, чтобы позже сравнить его и оценить экономию памяти благодаря 8-битной квантизации.
!pip install -q bitsandbytes>=0.39.0
!pip install -q git+https://github.com/huggingface/accelerate.git
!pip install -q git+https://github.com/huggingface/transformers.git
from transformers import AutoModelForCausalLM, AutoTokenizer
import torch
torch.manual_seed(0)
# Устанавливаем устройство на CPU
device = 'cpu'
# Загружаем модель и токенизатор
model_id = 'gpt2'
model = AutoModelForCausalLM.from_pretrained(model_id).to(device)
tokenizer = AutoTokenizer.from_pretrained(model_id)
# Выводим размер модели
print(f"Размер модели: {model.get_memory_footprint():,} байт")Размер модели: 510,342,192 байт
Размер модели GPT-2 в формате FP32 составляет примерно 487 МБ. Следующий шаг — квантизация весов с использованием zero-point и absmax. В следующем примере мы применим эти техники к первому слою внимания GPT-2, чтобы увидеть результаты.
# Извлекаем веса первого слоя
weights = model.transformer.h[0].attn.c_attn.weight.data
print("Исходные веса:")
print(weights)
# Квантизуем слой с использованием absmax
weights_abs_quant, _ = absmax_quantize(weights)
print("\nКвантизованные веса (absmax):")
print(weights_abs_quant)
# Квантизуем слой с использованием zero-point
weights_zp_quant, _ = zeropoint_quantize(weights)
print("\nКвантизованные веса (zero-point):")
print(weights_zp_quant)Исходные веса:
tensor([[-0.4738, -0.2614, -0.0978, ..., 0.0513, -0.0584, 0.0250],
[ 0.0874, 0.1473, 0.2387, ..., -0.0525, -0.0113, -0.0156],
[ 0.0039, 0.0695, 0.3668, ..., 0.1143, 0.0363, -0.0318],
...,
[-0.2592, -0.0164, 0.1991, ..., 0.0095, -0.0516, 0.0319],
[ 0.1517, 0.2170, 0.1043, ..., 0.0293, -0.0429, -0.0475],
[-0.4100, -0.1924, -0.2400, ..., -0.0046, 0.0070, 0.0198]])Квантизованные веса (absmax):
tensor([[-21, -12, -4, ..., 2, -3, 1],
[ 4, 7, 11, ..., -2, -1, -1],
[ 0, 3, 16, ..., 5, 2, -1],
...,
[-12, -1, 9, ..., 0, -2, 1],
[ 7, 10, 5, ..., 1, -2, -2],
[-18, -9, -11, ..., 0, 0, 1]], dtype=torch.int8)Квантизованные веса (zero-point):
tensor([[-20, -11, -3, ..., 3, -2, 2],
[ 5, 8, 12, ..., -1, 0, 0],
[ 1, 4, 18, ..., 6, 3, 0],
...,
[-11, 0, 10, ..., 1, -1, 2],
[ 8, 11, 6, ..., 2, -1, -1],
[-18, -8, -10, ..., 1, 1, 2]], dtype=torch.int8)Разница между исходными (FP32) и квантизованными (INT8) значениями очевидна, но разница между absmax и zero-point весами более тонкая. В этом случае входные данные выглядят сдвинутыми на значение -1, что говорит о довольно симметричном распределении весов в этом слое.
Теперь квантизуем все слои в GPT-2 (линейные слои, слои внимания и т.д.) и создадим две новые модели: model_abs и model_zp. Для точности заменим исходные веса на деквантизованные. Это даёт два преимущества: 1) позволяет сравнить распределение весов (в одном масштабе) и 2) фактически запустить модели.
PyTorch по умолчанию не поддерживает умножение матриц в INT8 на CPU (центральном процессоре). В реальном сценарии мы бы деквантизовали их для запуска модели (например, в FP16), но хранили бы их в INT8. В следующем разделе мы используем библиотеку bitsandbytes для решения этой проблемы.
import numpy as np
from copy import deepcopy
# Сохраняем исходные веса
weights = [param.data.clone() for param in model.parameters()]
# Создаём модель для квантизации
model_abs = deepcopy(model)
# Квантизуем все веса модели
weights_abs = []
for param in model_abs.parameters():
_, dequantized = absmax_quantize(param.data)
param.data = dequantized
weights_abs.append(dequantized)
# Создаём модель для квантизации
model_zp = deepcopy(model)
# Квантизуем все веса модели
weights_zp = []
for param in model_zp.parameters():
_, dequantized = zeropoint_quantize(param.data)
param.data = dequantized
weights_zp.append(dequantized)Теперь, когда наши модели квантизованы, мы хотим оценить влияние этого процесса. Интуитивно понятно, что квантизованные веса должны быть близки к исходным. Визуально это можно проверить, построив распределение деквантизованных и исходных весов. Если квантизация приводит к значительным потерям, это сильно изменит распределение весов.
На следующем графике показано это сравнение: синяя гистограмма представляет исходные (FP32) веса, а красная — деквантизованные (из INT8) веса. Обратите внимание, что мы отображаем график только в диапазоне от -2 до 2 из-за выбросов с очень большими абсолютными значениями (об этом позже).
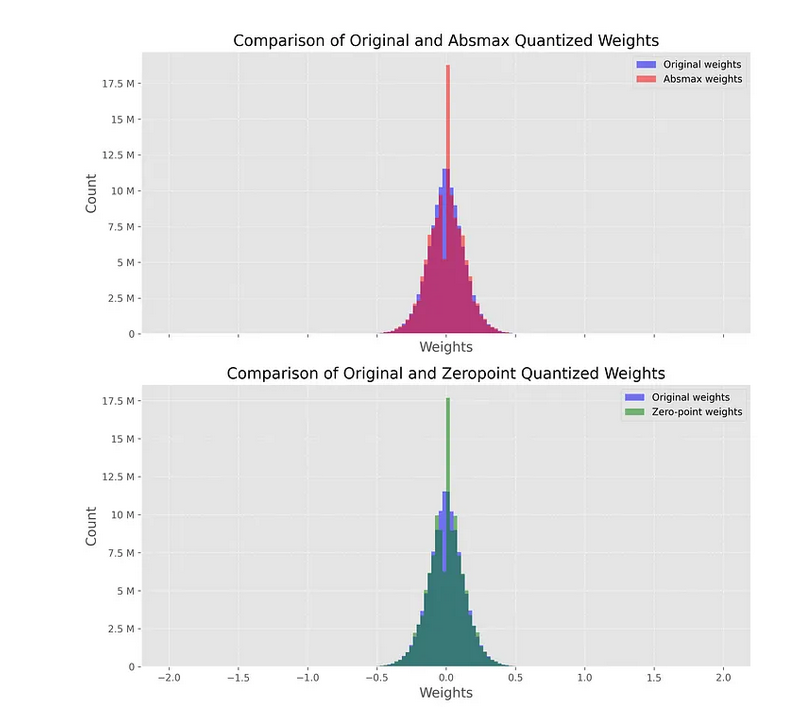
Рис. 6. Сравнение распределений весов модели - исходных и полученных после деквантования
Оба графика довольно похожи, с заметным пиком вокруг 0. Этот пик показывает, что наша квантизация приводит к значительным потерям, так как обратное преобразование не восстанавливает исходные значения. Это особенно верно для модели absmax, которая демонстрирует как более быстрое падение хвостов, так и более высокий пик вокруг 0.
Сравним качество исходной и квантизованных моделей. Для этого определим функцию generate_text(), которая генерирует 50 токенов с использованием top-k сэмплирования.
def generate_text(model, input_text, max_length=50):
input_ids = tokenizer.encode(input_text, return_tensors='pt').to(device)
output = model.generate(inputs=input_ids,
max_length=max_length,
do_sample=True,
top_k=30,
pad_token_id=tokenizer.eos_token_id,
attention_mask=input_ids.new_ones(input_ids.shape))
return tokenizer.decode(output[0], skip_special_tokens=True)
# Генерируем текст с исходной и квантизованными моделями
original_text = generate_text(model, "I have a dream")
absmax_text = generate_text(model_abs, "I have a dream")
zp_text = generate_text(model_zp, "I have a dream")
print(f"Исходная модель:\n{original_text}")
print("-" * 50)
print(f"Модель (absmax):\n{absmax_text}")
print("-" * 50)
print(f"Модель (zero-point):\n{zp_text}")Исходная модель:
I have a dream, and it is a dream I believe I would get to live in my future. I love my mother, and there was that one time I had been told that my family wasn't even that strong. And then I got theМодель (absmax):
I have a dream to find out the origin of her hair. She loves it. But there's no way you could be honest about how her hair is made. She must be crazy.
We found a photo of the hairstyle posted on
Модель (zero-point):
I have a dream of creating two full-time jobs in America—one for people with mental health issues, and one for people who do not suffer from mental illness—or at least have an employment and family history of substance abuse, to work partВместо того чтобы пытаться определить, какой вывод имеет больше смысла, мы можем количественно оценить его, рассчитав перплексию для каждого вывода. Это распространённая метрика для оценки языковых моделей, которая измеряет неопределённость модели в предсказании следующего токена в последовательности. В этом сравнении мы предполагаем, что чем ниже показатель, тем лучше модель. На практике предложение с высокой перплексией также может быть корректным.
Реализуем её с помощью простой функции, так как нам не нужно учитывать детали, такие как длина контекстного окна, поскольку наши предложения короткие.
def calculate_perplexity(model, text):
# Кодируем текст
encodings = tokenizer(text, return_tensors='pt').to(device)
# Определяем input_ids и target_ids
input_ids = encodings.input_ids
target_ids = input_ids.clone()
with torch.no_grad():
outputs = model(input_ids, labels=target_ids)
# Вычисляем потери
neg_log_likelihood = outputs.loss
# Вычисляем перплексию
ppl = torch.exp(neg_log_likelihood)
return ppl
ppl = calculate_perplexity(model, original_text)
ppl_abs = calculate_perplexity(model_abs, absmax_text)
ppl_zp = calculate_perplexity(model_zp, absmax_text)
print(f"Перплексия (исходная): {ppl.item():.2f}")
print(f"Перплексия (absmax): {ppl_abs.item():.2f}")
print(f"Перплексия (zero-point): {ppl_zp.item():.2f}")- Перплексия (исходная): 15.53
- Перплексия (absmax): 17.92
- Перплексия (zero-point): 17.97
Мы видим, что перплексия исходной модели немного ниже, чем у двух других. Один эксперимент не очень надёжен, но мы могли бы повторить этот процесс несколько раз, чтобы увидеть разницу между моделями. В теории zero-point квантизация должна быть немного лучше, чем absmax, но она также более затратна с точки зрения вычислений.
В этом примере мы применили техники квантизации ко всем слоям (на основе тензора). Однако можно применять их на разных уровнях гранулярности: от всей модели до отдельных значений. Квантизация всей модели за один проход серьёзно ухудшит качество, тогда как квантизация отдельных значений создаст большую нагрузку. На практике часто предпочитают векторизованную квантизацию (векторное квантование), которая учитывает изменчивость значений в строках и столбцах внутри одного тензора.
Однако даже векторизованная квантизация не решает проблему выбросов. Выбросы — это экстремальные значения (положительные или отрицательные), которые появляются во всех слоях трансформеров, когда модель достигает определённого масштаба (> нескольких млрд параметров). Это проблема, так как один выброс может снизить точность для всех остальных значений. Но отбрасывать эти выбросы нельзя, так как это серьёзно ухудшит качество модели.
8-битная квантизация с LLM.int8()
Предложенная Dettmers et al. (2022), LLM.int8() — это решение проблемы выбросов. Она основана на схеме векторизованной (absmax) квантизации и вводит квантизацию со смешанной точностью. Это означает, что выбросы обрабатываются в формате FP16, чтобы сохранить их точность, а остальные значения — в формате INT8. Поскольку выбросы составляют около 0.1% значений, это эффективно сокращает использование памяти LLM почти в 2 раза.
(Нажмите Enter или кликните, чтобы увидеть изображение в полном размере)
LLM.int8() работает, выполняя вычисление умножения матриц в три ключевых шага:
- Извлекает столбцы из входных скрытых состояний X, содержащих выбросы, используя пользовательский порог.
- Выполняет умножение матриц для выбросов в FP16, а для остальных значений — в INT8 с векторизованной квантизацией (по строкам для скрытого состояния X и по столбцам для матрицы весов W).
- Деквантизует результаты для невыбросов (INT8 в FP16) и добавляет их к результатам для выбросов, чтобы получить полный результат в FP16.
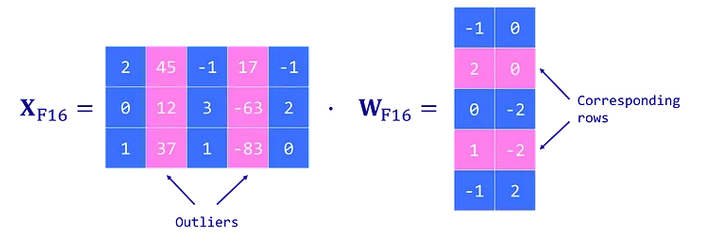
Рис. 7. Обработка выбросов
Этот подход необходим, потому что 8-битная точность ограничена и может приводить к существенным ошибкам при квантизации вектора с большими значениями. Эти ошибки также имеют тенденцию усиливаться при распространении через несколько слоёв.
Мы можем легко использовать эту технику благодаря интеграции библиотеки bitsandbytes в экосистему Hugging Face. Достаточно указать load_in_8bit=True при загрузке модели (также требуется GPU).
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model_int8 = AutoModelForCausalLM.from_pretrained(model_id,
device_map='auto',
load_in_8bit=True,
)
print(f"Размер модели: {model_int8.get_memory_footprint():,} байт")Размер модели: 176,527,896 байт
С этой дополнительной строкой кода модель теперь почти в три раза меньше (168 МБ против 487 МБ). Мы даже можем сравнить распределение исходных и квантизованных весов, как делали ранее:
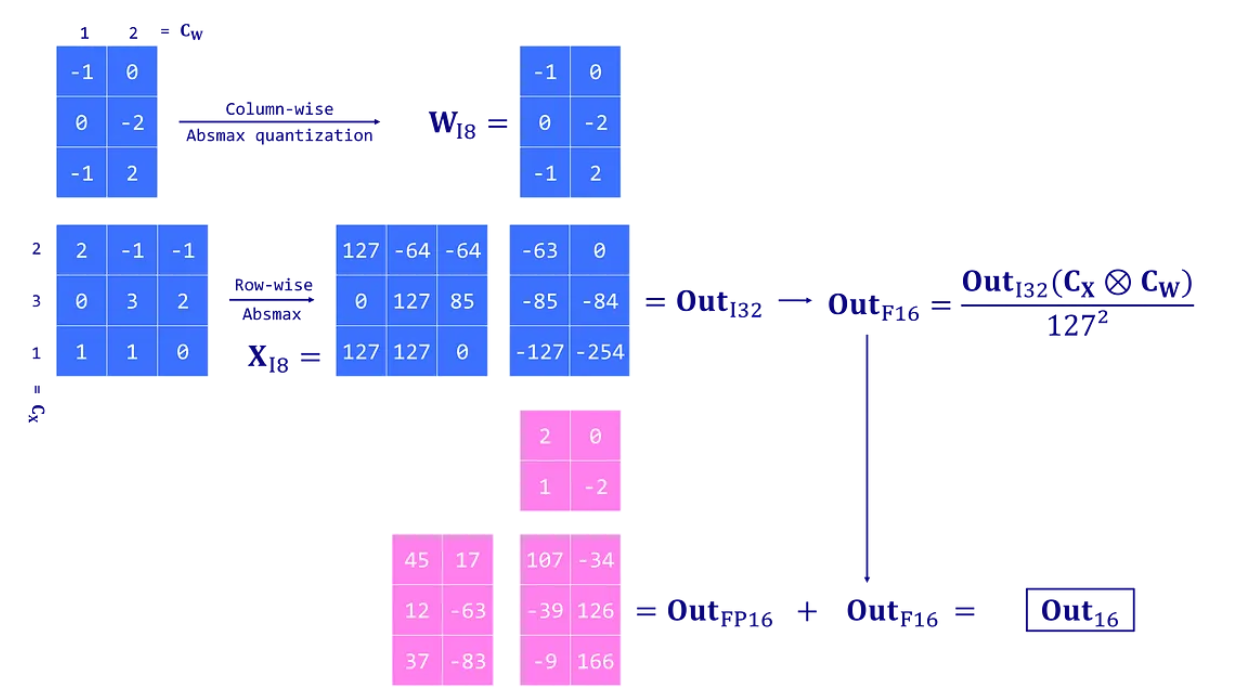
Рис. 8. Обработка выбросов - раздельно в int8 и int32 - для целочисленно квантованных и в fp16 для строк и столбцов с выбросами
В этом случае мы видим пики вокруг -2, -1, 0, 1, 2 и т.д. Эти значения соответствуют параметрам, хранящимся в формате INT8 (невыбросы). Вы можете убедиться в этом, распечатав веса модели с помощью model_int8.parameters().
Мы также можем сгенерировать текст с этой квантизованной моделью и сравнить его с исходной моделью.
# Генерируем текст с квантизованной моделью
text_int8 = generate_text(model_int8, "I have a dream")
print(f"Исходная модель:\n{original_text}")
print("-" * 50)
print(f"Модель (LLM.int8()):\n{text_int8}")Исходная модель:
I have a dream, and it is a dream I believe I would get to live in my future. I love my mother, and there was that one time I had been told that my family wasn't even that strong. And then I got theМодель (LLM.int8()):
I have a dream. I don't know what will come of it, but I am going to have to look for something that will be right. I haven't thought about it for a long time, but I have to try to get that thingСнова сложно судить, какой вывод лучше, но мы можем положиться на метрику перплексии, чтобы получить (приблизительный) ответ.
print(f"Перплексия (исходная): {ppl.item():.2f}")
ppl = calculate_perplexity(model_int8, text_int8)
print(f"Перплексия (LLM.int8()): {ppl.item():.2f}")- Перплексия (исходная): 15.53
- Перплексия (LLM.int8()): 7.93
В этом случае перплексия квантизованной модели в два раза ниже, чем у исходной. Обычно так не бывает, но это показывает, что данная техника квантизации очень конкурентоспособна. Авторы LLM.int8() демонстрируют, что деградация производительности настолько мала, что ею можно пренебречь (<1%). Однако это связано с дополнительными вычислительными затратами: LLM.int8() примерно на 20% медленнее для крупных моделей.
Bitsandbytes
В этой статье представлен обзор самых базовых техник квантизации весов. Мы начали с изучения представления чисел с плавающей запятой, затем рассмотрели две техники 8-битной квантизации: absmax и zero-point. Однако их ограничения, особенно в обработке выбросов, привели к созданию LLM.int8() — техники, которая также сохраняет качество модели. Этот подход подчёркивает прогресс в области квантизации весов и важность правильной обработки выбросов.
LLM.int8() реализован в библиотекре bitsandbytes
Библиотека bitsandbytes обеспечивает доступность больших языковых моделей за счёт квантований разрядности k бит для PyTorch. В ней реализованы три основные функции, позволяющие значительно сократить потребление памяти при выводе (inference) и обучении:
- 8-битные оптимизаторы используют блочное квантование, чтобы сохранять производительность на уровне 32-битных вычислений при значительно меньших затратах памяти.
- LLM.int8() или 8-битное квантование позволяет выполнять вывод в крупных языковых моделях, используя лишь половину требуемой памяти, без потери качества. Данный метод основан на поэлементном (векторном) квантовании, переводящем большинство параметров в 8-битный формат, при этом выбросы обрабатываются отдельно с использованием матричного умножения в 16-битной точности.
- QLoRA или 4-битное квантование позволяет обучать крупные языковые модели, применяя несколько методов экономии памяти без ущерба для производительности. Этот метод квантует модель до 4 бит и добавляет небольшой набор обучаемых весов с низким рангом (low-rank adaptation, LoRA), что делает обучение возможным.
Библиотека включает примитивы квантования для операций с 8 и 4 битами через классы bitsandbytes.nn.Linear8bitLt и bitsandbytes.nn.Linear4bit, а также 8-битные оптимизаторы — через модуль bitsandbytes.optim.
Блочное квантование реализовано с помощью блоков размером 256 значений. Изначально, в оригинальной реализации, использовался размер блока 2048.
Основные параметры квантования
При использовании библиотеки bitsandbytes с Hugging Face Transformers несколько параметров управляют процессом квантования:
- load_in_8bit (bool): Если установлено значение True, веса модели загружаются и квантуются до 8 бит.
- load_in_4bit (bool): Если установлено значение True, веса модели загружаются и квантуются до 4 бит.
- bnb_4bit_quant_type (str): Определяет тип 4-битного квантования. Распространенные варианты:
- "nf4" (NormalFloat4): Значение по умолчанию, рекомендуется к использованию. Информационно-теоретически оптимальный формат данных для нормально распределенных весов.
- "fp4" (FloatPoint4): Альтернативное 4-битное представление с плавающей запятой.
- bnb_4bit_use_double_quant (bool): Включает двойное квантование, при котором константы квантования сами подвергаются дополнительному квантованию. Это позволяет дополнительно сэкономить в среднем 0,4 бита на параметр.
- bnb_4bit_compute_dtype (torch.dtype): Определяет тип данных, используемый для вычислений в прямом и обратном проходах (для QLoRA). Распространенные варианты: torch.float16 или torch.bfloat16. Использование типа данных с более высокой точностью для вычислений помогает сохранить производительность модели при хранении весов в 4-битном формате.
Bitsandbytes использует квантование на лету (in-flight/on-the-fly quantization): основной и наиболее распространенный способ использования bitsandbytes заключается в том, что библиотека загружает оригинальные веса модели с полной точностью и автоматически квантует их в 8-бит или 4-бит формат во время загрузки модели. Это происходит без необходимости калибровочного датасета или дополнительной обработки — веса автоматически квантуются при загрузке.
При использовании с библиотекой Transformers достаточно указать конфигурацию квантования во время загрузки модели (например, параметр load_in_4bit=True), и bitsandbytes автоматически выполнит квантование на лету. Это позволяет значительно сократить использование памяти и работать с большими моделями, не требуя предварительного сохранения квантованной версии модели.
Основной сценарий использования bitsandbytes — это квантование на лету, хотя технически поддерживается и загрузка предварительно квантованных моделей.
Блочное квантование
Блочное квантование (block-wise quantization) в библиотеке bitsandbytes — это метод квантования, при котором веса модели или градиенты разделяются на фиксированные подмножества (блоки), и для каждого блока независимо вычисляются параметры квантования (масштаб и сдвиг). Это позволяет минимизировать ошибку квантования за счет адаптации к локальной статистике данных в пределах блока, сохраняя при этом совместимость с низкоразрядными вычислениями (8 бит).
Блок квантования — это последовательный сегмент весов или градиентов фиксированного размера (в текущей версии библиотеки 256 элементов), обрабатываемый как единая единица при квантовании. Для каждого блока:
- Вычисляется локальный масштаб (scale factor), нормализующий значения в блоке к диапазону, представимому в 8-битной арифметике.
- Применяется аффинное преобразование (квантование):
\[ Q(x) = \text{round}\left(\frac{x}{\text{scale}}\right) + \text{zero_point}\]
где \(Q(x)\) — квантованное значение, а zero_point корректирует смещение для несимметричного диапазона.
Зачем это нужно?
- Снижение ошибки квантования: Глобальное квантование (единый масштаб для всех весов) приводит к большим погрешностям, если веса имеют неоднородное распределение (например, комбинация малых и крупных значений). Блочное квантование адаптируется к локальной дисперсии, сохраняя точность.
- Совместимость с 32-битной версией: При использовании 8-битных оптимизаторов (например, Adam8bit) градиенты и состояния оптимизатора хранятся в 8 бит, но вычисления (например, обновление весов) выполняются в 32 битах. Блочное квантование обеспечивает минимальную потерю точности на этапе хранения.
- Экономия памяти: Для 8-битных оптимизаторов память под состояния (моменты, экспоненциальные скользящие средние) сокращается на ~75% по сравнению с 32-битной реализацией.
Блочное квантование минимизирует среднеквадратичную ошибку (MSE) в пределах блока за счет выбора оптимального масштаба:
\[ \text{scale} = \frac{2 \cdot \max(|x_i|)}{2^b - 1}, \quad i \in \text{block}\]
где \(b\) — целевая разрядность (8 бит), а \(\max(|x_i|)\) вычисляется локально для блока.
Пример работы
Для тензора градиентов \(G = [g_1, g_2, ..., g_{1024}]\):
- Тензор делится на \(1024 / 256 = 4\) блока.
- Для каждого блока \(B_k\) вычисляется свой масштаб \(s_k = \max(|B_k|) / 127\).
- Градиенты в блоке квантуются в случае симметричного квантования: \(Q(B_k) = \text{round}(B_k / s_k)\).
- При обновлении весов: \(\Delta W = \text{dequantize}(Q(B_k)) \cdot \text{learning_rate}\).
Ключевое отличие от других методов
- Глобальное квантование: один масштаб для всего тензора → высокая ошибка для неоднородных данных.
- Блочное квантование: локальные масштабы → точность близка к 32 битам даже при 8-битном хранении.
- Векторное квантование (LLM.int8()): масштаб вычисляется для каждого вектора активаций (а не для фиксированных блоков весов).
Блочное и векторное квантование
В контексте квантования языковых моделей (LLM), такие термины, как блочное квантование и векторное квантование, относятся к разным подходам снижения точности весов модели для уменьшения размера и ускорения инференса. Однако важно понимать, что эти термины не всегда используются строго одинаково в разных источниках — иногда они могут пересекаться или использоваться в разных контекстах.
Блочное квантование (Block-wise Quantization)
- Веса модели делятся на блоки (например, по строкам, столбцам или подматрицам), и каждый блок квантуется независимо, с собственной шкалой (scale) и/или сдвигом (zero point).
- Часто используется в методах типа GPTQ, SmoothQuant, LLM.int8(), AWQ и т.п.
Пример:
- Блок = 128 последовательных весов в одном столбце матрицы.
- Для каждого блока вычисляется свой коэффициент масштабирования: \(Q = \text{round}(W / s)\), где \(s\) — масштаб, зависящий от диапазона значений в этом блоке.
Преимущества:
- Лучшая точность по сравнению с глобальным квантованием, потому что адаптируется к локальной статистике весов.
- Учитывает то, что разные части модели (например, разные каналы) могут иметь сильно отличающиеся распределения весов.
Недостатки:
- Требуется хранить дополнительные параметры (масштабы, zero points) для каждого блока → накладные расходы.
- Сложнее реализовать на некоторых устройствах из-за переменной шкалы.
Векторное квантование (Vector Quantization, VQ)
Что это:
- Группировка весов в векторы (например, группы весов, соответствующие одному нейрону или фиче), и затем замена этих векторов на ближайший кодовый вектор из заранее определённого кодбука (codebook).
- Это более агрессивная форма квантования, чем скалярное (по одному весу) или блочное.
Пример:
- Представим, что у нас есть вектор весов \(\mathbf{w} \in \mathbb{R}^d\). Мы заменяем его на ближайший вектор \(\mathbf{c}_k\) из кодбука \(C = \{\mathbf{c}_1, ..., \mathbf{c}_K\}\): \(\mathbf{w} \approx \mathbf{c}_k\)
Использование в LLM:
- Реже применяется напрямую к весам полных LLM, чаще используется в сжатии активаций, эмбеддингах или в VQ-VAE.
- Может применяться при сжатии ключевых компонентов, например, ключей/значений в attention.
Преимущества:
- Очень высокая степень сжатия: вместо хранения вектора хранится лишь индекс в кодбуке.
- Позволяет обнаруживать повторяющиеся паттерны в весах.
Недостатки:
- Высокая вычислительная сложность (поиск ближайшего соседа в кодбуке).
- Потеря точности может быть значительной.
- Обучение кодбука требует дополнительных усилий (например, k-means или обучение end-to-end).
Ключевые отличия
| Характеристика | Блочное квантование | Векторное квантование |
|---|---|---|
| Единица обработки | Блок скалярных весов (например, 32, 64, 128 элементов) | Вектор признаков (группа весов как единый объект) |
| Тип квантования | Скалярное квантование с локальными параметрами | Замена вектора на эталон из codebook |
| Параметры | Масштаб и ноль для каждого блока | Кодбуки (codebooks) и индексы |
| Сжатие | Умеренное (например, 4 бита/вес) | Высокое (log₂(K) бит на вектор) |
| Точность | Относительно высокая | Может быть ниже, особенно при малом K |
| Использование в LLM | Широко (GPTQ, AWQ, etc.) | Ограниченно (чаще в эмбеддингах, активациях) |
Аналогия
- Блочное квантование — как если бы вы сканировали изображение полосами и для каждой полосы выбирали свой контраст/яркость.
- Векторное квантование — как если бы вы заменяли каждые 4 пикселя на один из 256 заранее заданных паттернов.
Хороших вам квантований!
