4-битное квантование с использованием GPTQ - Generalized Post-Training Quantization

https://arxiv.org/abs/2210.17323 - GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers

https://huggingface.co/docs/transformers/main/en/quantization/gptq

Недавние достижения в области квантования весов позволяют запускать огромные языковые модели на потребительском оборудовании, например, модель LLaMA-30B на графическом процессоре RTX 3090. Это стало возможным благодаря новым методам 4-битного квантования с минимальным снижением производительности, таким как GPTQ, GGML и NF4.

Ранее мы рассмотрели наивные методы 8-битного квантования и отличную библиотеку bitsandbytes, реализующую подход LLM.int8(). Важно понимать ограничения базовой пост-обучающей квантизации (Post-Training Quantization, PTQ). Простые методы, такие как округление весов до ближайшего целого значения, часто не сохраняют точность модели, особенно при очень низкой разрядности, например, INT4. Большие языковые модели (LLM) особенно чувствительны к этому, поскольку небольшие ошибки в одном слое могут накапливаться и усиливать ошибки в последующих слоях.

GPTQ (Generalized Post-Training Quantization, обобщённая пост-обучающая квантизация) была разработана для решения проблемы потери точности. Вместо квантизации каждого веса независимо, GPTQ оптимизирует процесс квантизации для всей матрицы весов слоя сразу, стремясь минимизировать ошибку, вносимую в выходные данные слоя. Это более сложный подход, который обеспечивает значительно более высокую точность по сравнению с базовыми методами PTQ, часто сопоставимую с производительностью исходной модели FP32, без необходимости повторного обучения.

Начнем с постановки задачи, которую мы пытаемся решить. Для каждого слоя ℓ в сети мы хотим найти квантованную версию Ŵₗ исходных весов Wₗ. Это называется задачей послойного сжатия. Более конкретно, чтобы минимизировать снижение производительности, мы хотим, чтобы выходы (ŴᵨXᵨ) этих новых весов были как можно ближе к исходным (WᵨXᵨ). Другими словами, мы хотим найти:

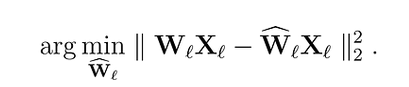
Рис. 1. Подбираем веса, которые на некотором наборе данных дадут меньшее отклонение от исходной модели

GPTQ (Generative Pre-trained Transformer Quantization) представляет собой метод посттренировочного квантования (Post-Training Quantization, PTQ), разработанный специально для оптимизации больших языковых моделей. В отличие от методов, требующих повторного обучения (Quantization-Aware Training), GPTQ работает с уже обученной моделью, минимизируя потери точности при снижении битности представления весов.

Основная цель GPTQ — преобразовать веса модели из 16-битного или 32-битного формата в более компактные представления (обычно 2-8 бит), сохраняя при этом высокую точность генерации. Алгоритм получил широкое распространение благодаря своей способности эффективно квантовать LLM в 4-битную точность с минимальными потерями качества.

Послойная обработка

GPTQ реализует послоевой подход к квантованию, где веса обрабатываются один слой за другим в изоляции. Это ключевое отличие от методов, обрабатывающих всю модель целиком, и позволяет более точно контролировать ошибку квантования на каждом этапе.

Алгоритм оптимизирует процесс квантования для всей матрицы весов слоя одновременно, стремясь минимизировать ошибку, вносимую в выходные данные слоя. Такой подход гарантирует, что ошибка квантования не накапливается катастрофически при переходе от слоя к слою.

Центральным элементом GPTQ является минимизация среднеквадратической ошибки (MSE) между полноточной и квантованной версиями слоя на некотором наборе данных. Для этого алгоритм использует калибровочный набор данных (обычно небольшой подмножество обучающих данных), чтобы оценить статистику активаций и определить оптимальные параметры квантования.

В оригинальной работе Frantar et al. (2022) представлен полный псевдокод алгоритма GPTQ, включающий все оптимизации и математические выкладки, лежащие в основе метода. Алгоритм обрабатывает веса по столбцам в блоках фиксированного размера B, для каждого столбца внутри блока вычисляя и минимизируя ошибку квантования на предложенных калибровочных данных.

Процесс квантования

1. Инициализация: Загрузка предобученной модели и выбор калибровочного набора данных

2. Послойная обработка (начиная с последнего слоя):

   • Для каждого слоя собирается статистика активаций на калибровочном наборе
   • Вычисляется обратная ковариационная матрица активаций
   • Оптимизируются параметры квантования (масштаб и смещение) для минимизации ошибки

3. Блочное квантование:

   • GPTQ выполняет квантование по столбцам в блоках определенного размера
   • Для каждого столбца внутри блока вычисляется ошибка квантования и корректируются параметры
   • В некоторых реализациях (например, AutoGPTQ) каждая строка матрицы весов квантует независимо для нахождения оптимальной версии весов

4. Коррекция ошибки: После квантования каждого слоя ошибка распространяется на последующие слои, что учитывается при квантовании следующих слоев

GPTQ поддерживает как симметричное, так и асимметричное квантование, что позволяет более точно представлять распределение весов. Алгоритм особенно эффективен при 4-битном квантовании, где традиционные методы часто приводят к значительным потерям качества.

Одним из ключевых преимуществ GPTQ является его способность обрабатывать веса слоя целиком, а не отдельные тензоры, что позволяет учитывать взаимосвязи между различными компонентами слоя и минимизировать суммарную ошибку.

В отличие от метода bitsandbytes, который использует квантование per-token, GPTQ применяет послоевую оптимизацию с учетом статистики активаций на общем наборе калибровочных данных. По сравнению с AWQ (Activation-Aware Weight Quantization), GPTQ не требует сложных эвристик для определения важности весов, вместо этого используя прямую оптимизацию ошибки.

Результаты оценки различных методов квантования показывают, что GPTQ обеспечивает хороший компромисс между точностью и степенью сжатия, особенно для моделей с большим количеством параметров.

Для практического применения GPTQ чаще всего используется библиотека AutoGPTQ, которая предоставляет удобный интерфейс для квантования популярных архитектур LLM. Процесс включает выбор базовой модели, подготовку калибровочного набора данных, настройку параметров квантования (битность, блочный размер) и запуск процедуры квантования.

Реализация GPTQ позволяет сократить размер модели до 4-кратного (при 4-битном квантовании) с потерей точности всего в 1-2% по сравнению с полноточной версией, что делает его одним из популярных методов посттренировочного квантования на сегодняшний день.

Проблема квантизации на уровне слоя

GPTQ работает со слоями поочерёдно. Рассмотрим линейный слой в LLM, операция которого определяется матричным умножением:

\(Y = WX\)

Здесь:

• W — исходная матрица весов полной точности,
• X — входные активации (из предыдущего слоя или начальные эмбеддинги),
• Y — выходные активации.

При квантизации весов до более низкой точности, например, INT4, получаем квантизованную матрицу весов \(W_Q\). Цель PTQ — найти такую \(W_Q\), чтобы выходные данные \(W_QX\) были максимально близки к исходным выходным данным \(WX\).

Ошибка, вносимая квантизацией в этом слое, может быть измерена среднеквадратичной ошибкой (MSE) между исходными и квантизованными выходными данными:

\(\text{Error} = \|WX - W_QX\|_F^2\)

где \(\| \cdot \|_F^2\) обозначает квадрат нормы Фробениуса (сумма квадратов разностей всех элементов). Базовые методы PTQ, такие как округление до ближайшего (RTN), определяют каждый элемент в \(W_Q\) независимо, обычно просто округляя соответствующий элемент в \(W\). Такой жадный подход не учитывает структуру входных данных \(X\) или взаимодействие между весами при минимизации общей ошибки выходных данных.

Последовательная квантизация и компенсация ошибок

GPTQ использует более аккуратный итеративный подход. Он квантизует веса внутри слоя последовательно, часто столбец за столбцом (или иногда строка за строкой, или небольшими блоками). Ключевая идея — компенсация ошибок: после квантизации конкретного веса (или группы весов) GPTQ вычисляет ошибку, вносимую этим шагом квантизации, и немедленно обновляет оставшиеся, ещё не квантизованные веса в слое, чтобы компенсировать эту ошибку.

Представьте, что мы квантизуем столбцы матрицы весов \(W\) по одному:

1. Выбираем первый столбец \(w_1\).
2. Находим оптимальное квантизованное значение \(w_{q1}\) для этого столбца. Это не обязательно просто округление; значение выбирается так, чтобы минимизировать ошибку реконструкции \(\|w_1x_1 - w_{q1}x_1\|^2\), потенциально учитывая его влияние на остальную часть слоя.
3. Вычисляем ошибку квантизации для этого столбца: \(E_1 = (w_1 - w_{q1})X\).
4. Ключевой момент: корректируем оставшиеся неквантизованные столбцы (\(w_2, w_3, \dots\)), чтобы компенсировать \(E_1\). Цель — изменить эти столбцы так, чтобы их совокупный выходной сигнал при умножении на \(X\) помог сгладить ошибку \(E_1\).
5. Переходим к следующему столбцу \(w_2\), квантизуем его, вычисляем ошибку \(E_2\), обновляем оставшиеся столбцы (\(w_3, w_4, \dots\)) и так далее.

Этот последовательный процесс гарантирует, что решения о квантизации, принятые на ранних этапах, компенсируются на последующих, что приводит к значительно меньшей общей ошибке реконструкции слоя по сравнению с независимым округлением.

Роль информации второго порядка (гессиана)

Как именно обновляются оставшиеся веса? Простое пропорциональное добавление ошибки обратно может быть неоптимальным. GPTQ использует приближённую информацию второго порядка о функции ошибки, а именно — матрицу Гессиана.

Цель — минимизировать квадратичную ошибку \(\|(W - W_Q)X\|^2\). Гессиан этой целевой функции относительно весов \(W\) даёт информацию о кривизне поверхности ошибки. Для линейного слоя этот гессиан \(H\) напрямую связан с входными активациями \(X\):

\(H = 2XX^T\)

Эта матрица \(XX^T\) представляет ковариацию входных признаков. Интуитивно она показывает, какие направления в пространстве входных данных наиболее важны или изменчивы на основе калибровочных данных.

GPTQ использует обратную матрицу Гессиана \(H^{-1}\), чтобы направлять шаг компенсации ошибки. Когда ошибка \(E\) вносится квантизацией веса, обновление, применяемое к оставшимся весам, пропорционально \(H^{-1}E\). Использование обратного Гессиана помогает приоритизировать корректировки вдоль направлений, которые наиболее чувствительны согласно статистике входных данных. Это позволяет более целенаправленно компенсировать ошибки, сосредотачивая корректировки там, где они окажут наибольшее влияние на уменьшение итоговой ошибки выходных данных.

Вычисление и обращение полного Гессиана может быть вычислительно затратным, особенно для больших слоёв. GPTQ использует эффективные численные методы и приближения (часто работая поблочно или используя итеративные решатели, такие как разложение Холецкого), чтобы сделать процесс выполнимым. Этот подход вдохновлён предыдущими работами, такими как Optimal Brain Surgeon и Optimal Brain Quantizer (OBQ), которые также использовали информацию Гессиана для обрезки и квантизации моделей.

Обзор алгоритма GPTQ

Приведём схему процесса GPTQ для матрицы весов одного слоя \(W\):

1. Инициализация: Начинаем с весов полной точности \(W\). Получаем представительный калибровочный набор данных \(X\).
2. Вычисление Гессиана: Рассчитываем Гессиан \(H = 2XX^T\) или его приближение с использованием калибровочных данных. Вычисляем его обратную матрицу \(H^{-1}\) (или подготавливаемся к эффективным обновлениям с её использованием).
3. Инициализация квантизованных весов: Устанавливаем \(W_Q = 0\) или некоторое начальное приближение. Отслеживаем, какие веса уже квантизованы.
4. Итеративная квантизация:
   • Для каждого веса (или столбца, или блока) \(w_i\) в \(W\):
     • Если \(w_i\) уже квантизован, переходим к следующему.
     • Определяем оптимальное квантизованное значение \(w_{qi}\) для \(w_i\). Это включает учёт текущей накопленной ошибки квантизации и влияние на выходные данные слоя, часто минимизируя \(\|(w_i - w_{qi})X + \text{AccumulatedError}\|^2\).
     • Вычисляем ошибку квантизации, вносимую этим шагом: \(\Delta_i = (w_i - w_{qi})\).
     • Обновляем оставшиеся неквантизованные веса \(w_j\) (где \(j > i\)) для компенсации этой ошибки. Правило обновления включает \(\Delta_i\) и обратный Гессиан \(H^{-1}\). Например, обновление для \(w_j\) может рассчитываться на основе соответствующих взаимодействий строк/столбцов, полученных из \(H^{-1}\).
     • Помечаем \(w_i\) как квантизованный (\(W_{Qi} = w_{qi}\)). Сохраняем вклад ошибки или обновляем накопленную ошибку.
     • В GPTQ для каждого столбца или строки матрицы весов может использоваться свой коэффициент масштабирования. Для матрицы размером 1000x1000 это может означать использование 1000 коэффициентов масштабирования. Для каждого квантуемого блока (столбца или строки) подбирается свой коэффициент масштабирования.
5. Завершение: После обработки всех весов \(W_Q\) — это финальная квантизованная матрица весов для слоя.

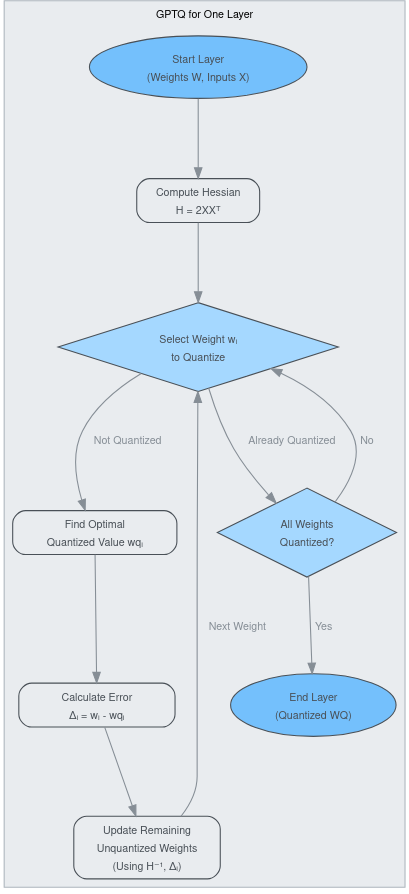
Рис. 1.1 Оптимизация слоя алгоритмом GPTQ

Калибровочные данные и гранулярность

GPTQ требует небольшого калибровочного набора данных (образцы входных активаций \(X\)) для вычисления Гессиана \(H = 2XX^T\). Качество и репрезентативность этого набора данных влияют на итоговую точность квантизации. Обычно достаточно нескольких сотен или тысяч образцов.

GPTQ часто применяется с групповой гранулярностью. Вместо квантизации весов по отдельности или столбец за столбцом, веса обрабатываются блоками (например, группами по 128). Это снижает вычислительные затраты на расчёты и обновления Гессиана, при этом обеспечивая значительно лучшие результаты по сравнению с квантизацией на уровне тензора или канала. Механизм компенсации ошибок применяется к этим группам.

Учитывая ошибку реконструкции слоя и используя статистику входных данных (через Гессиан) для направления компенсации ошибок, GPTQ минимизирует потерю точности гораздо эффективнее, чем более простые методы. Это делает его популярным выбором для достижения точной низкоразрядной квантизации весов в LLM.

Optimal Brain Quantizer

Осснову подхода составил фреймворк Optimal Brain Quantizer (OBQ). Этот метод вдохновлен техникой обрезки (pruning) для аккуратного удаления весов из полностью обученной плотной нейронной сети (Optimal Brain Surgeon). Он использует технику аппроксимации и предоставляет явные формулы для определения наилучшего одиночного веса \(w_{q}\) для удаления и оптимального обновления \(δ_{F}\) для корректировки оставшихся неквантованных весов F, чтобы компенсировать удаление:

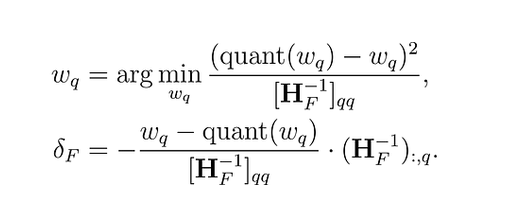
Рис. 2. Задача OBQ

где quant(w) — это округление веса, заданное квантованием, а \(H_{F}\) — гессиан.

С помощью OBQ мы можем сначала квантовать самый незначимый вес, а затем скорректировать все оставшиеся неквантованные веса, чтобы компенсировать потерю точности. Затем мы выбираем следующий вес для квантования и так далее.

Потенциальная проблема этого подхода заключается в наличии выбросов (outlier weights), которые могут привести к высокой ошибке квантования. Обычно такие выбросы квантуются последними, когда остается мало неквантованных весов, которые можно скорректировать для компенсации большой ошибки. Этот эффект может усугубляться, если некоторые веса выталкиваются за пределы сетки промежуточными обновлениями. Для предотвращения этого применяется простая эвристика: выбросы квантуются сразу же, как только появляются.

Этот процесс может быть вычислительно затратным, особенно для больших языковых моделей. Чтобы справиться с этим, метод OBQ использует трюк, который позволяет избежать повторного выполнения всех вычислений каждый раз, когда вес округляется. После квантования веса он корректирует матрицу, используемую в вычислениях (гессиан), удаляя строку и столбец, связанные с этим весом (с использованием гауссова исключения):

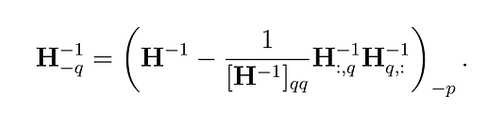
Рис. 3. Корректировка неквантованных весов для снижения ошибки квантования

Метод также использует векторизацию для одновременной обработки нескольких строк матрицы весов. Несмотря на свою эффективность, время вычислений OBQ значительно увеличивается с ростом размера матрицы весов. Этот кубический рост затрудняет использование OBQ на очень больших моделях с миллиардами параметров.

Алгоритм GPTQ

Представленный Frantar и др. (2023), алгоритм GPTQ вдохновлен методом OBQ, но с значительными улучшениями для масштабирования на (очень) большие языковые модели.

Шаг 1: Произвольный порядок

Метод OBQ выбирает веса (параметры модели) для квантования в определенном порядке, который зависит от того, какой из них добавит наименьшую дополнительную ошибку. Однако GPTQ замечает, что для больших моделей квантование весов в любом фиксированном порядке может работать так же хорошо. Это связано с тем, что, хотя некоторые веса могут вносить больше ошибок по отдельности, они квантуются позже в процессе, когда остается мало других весов, которые могли бы увеличить ошибку. Таким образом, порядок не так важен, как мы думали.

На основе этого наблюдения GPTQ стремится квантовать все веса в одном и том же порядке для всех строк матрицы. Это ускоряет процесс, так как некоторые вычисления нужно выполнять только один раз для каждого столбца, а не для каждого веса.

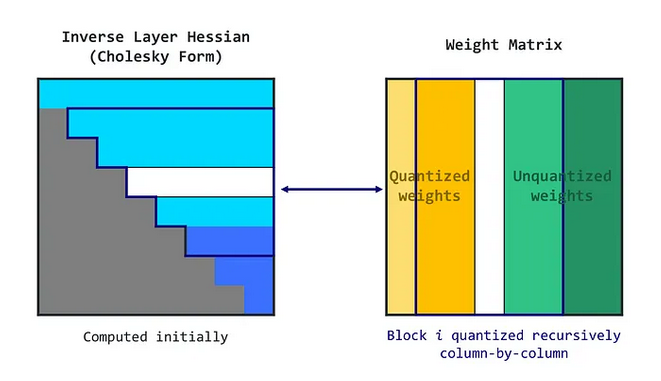
Рис. 4. Последовательное квантование с корректировками неквантованных весов

Шаг 2: Ленивые пакетные обновления (Lazy Batch-Updates)

Этот подход не будет быстрым, так как требует обновления огромной матрицы с очень небольшим количеством вычислений для каждого элемента. Такой тип операции не может полностью использовать вычислительные возможности GPU и будет замедлен ограничениями памяти (проблема пропускной способности памяти).

Чтобы решить эту проблему, GPTQ вводит "ленивые пакетные" обновления. Оказывается, что окончательные решения об округлении для данного столбца зависят только от обновлений, выполненных на этом столбце, а не на последующих столбцах. Поэтому GPTQ может применять алгоритм к пакету столбцов за раз (например, 128 столбцов), обновляя только эти столбцы и соответствующий блок матрицы. После полной обработки блока алгоритм выполняет глобальные обновления всей матрицы.

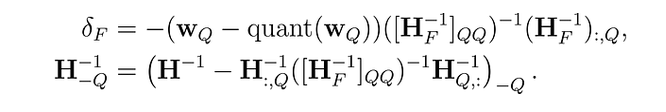
Рис. 5. Lazy Batch-Updates

Шаг 3: Переформулировка с использованием разложения Холецкого (Cholesky Reformulation)

Однако остается еще одна проблема. При масштабировании алгоритма на очень большие модели могут возникать численные неточности. В частности, повторное применение определенной операции может накапливать численные ошибки.

Для решения этой проблемы GPTQ использует разложение Холецкого — численно устойчивый метод решения определенных математических задач. Оно предполагает предварительное вычисление необходимой информации из матрицы с использованием метода Холецкого. Этот подход, в сочетании с небольшим "затуханием" (добавлением малой константы к диагональным элементам матрицы), помогает алгоритму избежать численных проблем.

Полный алгоритм можно кратко описать следующим образом:

• Алгоритм GPTQ начинается с разложения Холецкого обратного гессиана (матрицы, помогающей определить, как корректировать веса).
• Затем он работает в циклах, обрабатывая пакеты столбцов за раз.
• Для каждого столбца в пакете он квантует веса, подбирает коэффициент квантования, вычисляет ошибку и обновляет веса в блоке соответственно.
• После обработки пакета он обновляет все оставшиеся веса на основе ошибок блока.

Алгоритм GPTQ тестировался на различных задачах генерации текста. Он сравнивался с другими методами квантования, такими как округление всех весов до ближайшего квантованного значения (RTN). GPTQ использовался с семействами моделей BLOOM (176B параметров) и OPT (175B параметров), а модели квантовались с использованием одного графического процессора NVIDIA A100.

Квантование LLM с помощью AutoGPTQ

GPTQ стал очень популярен для создания моделей с 4-битной точностью, которые могут эффективно работать на GPU. Вы можете найти множество примеров на Hugging Face Hub, особенно от пользователя TheBloke. Если вы ищете подход, более дружелюбный к CPU, GGML на данный момент — лучше. Наконец, библиотека transformers с bitsandbytes позволяет квантовать модель при загрузке с использованием аргумента load_in_4bit=true, что требует загрузки полных моделей и их хранения в оперативной памяти.

Давайте реализуем алгоритм GPTQ с использованием библиотеки AutoGPTQ и квантуем модель GPT-2. Для этого потребуется GPU, но бесплатный T4 на Google Colab подойдет. Начнем с загрузки библиотек и определения модели, которую мы хотим квантовать (в данном случае GPT-2).

!BUILD_CUDA_EXT=0 pip install -q auto-gptq transformers
import random
from auto_gptq import AutoGPTQForCausalLM, BaseQuantizeConfig
from datasets import load_dataset
import torch
from transformers import AutoTokenizer

# Определяем базовую модель и выходной каталог
model_id = "gpt2"
out_dir = model_id + "-GPTQ"

Теперь мы хотим загрузить модель и токенайзер. Токенайзер загружается с использованием классического класса AutoTokenizer из библиотеки transformers. С другой стороны, для загрузки модели необходимо передать специфическую конфигурацию (BaseQuantizeConfig).

В этой конфигурации мы можем указать количество бит для квантования (здесь bits=4) и размер группы (размер ленивого пакета). Обратите внимание, что размер группы не является обязательным: мы могли бы также использовать один набор параметров для всей матрицы весов. На практике эти группы обычно улучшают качество квантования при очень низкой стоимости (особенно при group_size=1024). Значение damp_percent помогает разложению Холецкого и не должно изменяться.

Наконец, параметр desc_act (также называемый порядком активации) — это сложный параметр. Он позволяет обрабатывать строки на основе убывания активации, то есть наиболее важные или значимые строки (определяемые на основе входных и выходных данных) обрабатываются первыми. Этот метод направлен на размещение большей части ошибки квантования (неизбежно возникающей при квантовании) на менее значимых весах. Такой подход улучшает общую точность процесса квантования, обеспечивая обработку наиболее значимых весов с большей точностью. Однако при использовании вместе с размером группы desc_act может приводить к замедлению производительности из-за необходимости частого перезагрузки параметров квантования. По этой причине мы не будем использовать его здесь.

# Загружаем конфигурацию квантования, модель и токенайзер
quantize_config = BaseQuantizeConfig(
    bits=4,
    group_size=128,
    damp_percent=0.01,
    desc_act=False,
)
model = AutoGPTQForCausalLM.from_pretrained(model_id, quantize_config)
tokenizer = AutoTokenizer.from_pretrained(model_id)

Процесс квантования сильно зависит от выборок для оценки и улучшения качества квантования. Они предоставляют средство сравнения выходов, производимых оригинальной и новой квантованной моделями. Чем больше количество предоставленных выборок - данных на которых подбирается приближение исходной матрицы, тем выше потенциал для более точных и эффективных сравнений, что приводит к улучшению качества квантования.

В контексте этой статьи мы используем набор данных C4 (Colossal Clean Crawled Corpus) для генерации наших примеров для квантования. Набор данных C4 — это крупномасштабная, многоязычная коллекция веб-текстов, собранных из проекта Common Crawl. Этот обширный набор данных был очищен и подготовлен специально для обучения крупномасштабных языковых моделей, что делает его отличным ресурсом для таких задач. Другой популярной альтернативой является набор данных WikiText.

В следующем блоке кода мы загружаем 1024 примера из набора данных C4, токенизируем их и форматируем.

# Загружаем данные и токенизируем примеры
n_samples = 1024
data = load_dataset("allenai/c4", data_files="en/c4-train.00001-of-01024.json.gz", split=f"train[:{n_samples*5}]")
tokenized_data = tokenizer("\n\n".join(data['text']), return_tensors='pt')

# Форматируем токенизированные примеры
examples_ids = []
for _ in range(n_samples):
    i = random.randint(0, tokenized_data.input_ids.shape[1] - tokenizer.model_max_length - 1)
    j = i + tokenizer.model_max_length
    input_ids = tokenized_data.input_ids[:, i:j]
    attention_mask = torch.ones_like(input_ids)
    examples_ids.append({'input_ids': input_ids, 'attention_mask': attention_mask})

Теперь, когда набор данных готов, мы можем начать процесс квантования с размером пакета 1. После завершения мы сохраняем токенайзер и модель в формате safetensors.

# Квантуем с использованием GPTQ
model.quantize(
    examples_ids,
    batch_size=1,
    use_triton=True,
)

# Сохраняем модель и токенайзер
model.save_quantized(out_dir, use_safetensors=True)
tokenizer.save_pretrained(out_dir)

Как обычно, модель и токенайзер затем могут быть загружены из выходного каталога с использованием классов AutoGPTQForCausalLM и AutoTokenizer.

device = "cuda:0" if torch.cuda.is_available() else "cpu"

# Перезагружаем модель и токенайзер
model = AutoGPTQForCausalLM.from_quantized(
    out_dir,
    device=device,
    use_triton=True,
    use_safetensors=True,
)
tokenizer = AutoTokenizer.from_pretrained(out_dir)

Давайте проверим, что модель работает корректно. Модель AutoGPTQ (в основном) работает как обычная модель transformers, что делает её совместимой с пайплайнами генерации, как показано в следующем примере:

from transformers import pipeline

generator = pipeline('text-generation', model=model, tokenizer=tokenizer)
result = generator("I have a dream", do_sample=True, max_length=50)[0]['generated_text']
print(result)

Результат:

I have a dream," she told CNN last week. "I have this dream of helping my mother find her own. But, to tell that for the first time, now that I'm seeing my mother now, just knowing how wonderful it is that

Нам удалось получить убедительное продолжение от нашей квантованной модели GPT-2. Более глубокая оценка потребовала бы измерения перплексии квантованной модели по сравнению с оригинальной. Однако мы оставим это за рамками данной статьи.

Заключение

Мы рассмотрели алгоритм GPTQ — мощную технику квантования для запуска больших языковых моделей на потребительском GPU оборудовании. Мы показали, как он решает задачу послойного сжатия на основе улучшенной техники OBS с произвольным порядком, ленивыми пакетными обновлениями и переформулировкой Холецкого. Этот подход значительно снижает требования к памяти и вычислительным ресурсам, делая большие языковые модели доступными для более широкой аудитории.

Кроме того, мы можем квантовать модели LLM сами. Вы можете загрузить свою версию 4-битной квантованной модели GPTQ на Hugging Face Hub. Как упоминалось во введении, GPTQ — не единственный алгоритм 4-битного квантования: GGML и NF4 — отличные альтернативы с немного другими областями применения. Я рекомендую узнать о них больше и попробовать!