Зачем от LayerNorm перешли к RMSNorm
На основе https://arxiv.org/abs/1910.07467
Как эффективно обучать глубокие нейронные сети — это давняя задача. Для ускорения сходимости модели Ба и др. предложили нормализацию слоя (LayerNorm), которая стабилизирует обучение глубоких нейронных сетей, регулируя динамику нейронов внутри одного слоя с помощью статистик среднего и дисперсии. Благодаря своей простоте и отсутствию зависимостей между обучающими случаями, LayerNorm широко применяется в различных нейронных архитектурах, что обеспечивает значительный успех в различных задачах, начиная от компьютерного зрения, распознавания речи и заканчивая обработкой естественного языка. В некоторых случаях было обнаружено, что LayerNorm является необходимым для успешного обучения модели. Кроме того, отделение от выборок на основе пакетов наделяет LayerNorm превосходством над пакетной нормализацией (BatchNorm) при обработке последовательностей переменной длины с использованием рекуррентных нейронных сетей (RNN).
К сожалению, включение LayerNorm увеличивает вычислительные затраты. Хотя это незначительно для небольших и мелких нейронных моделей с небольшим количеством слоев нормализации, эта проблема становится серьезной, когда базовые сети становятся больше и глубже. В результате выигрыш в эффективности от более быстрого и стабильного обучения (с точки зрения количества шагов обучения) уравновешивается увеличением вычислительных затрат на шаг обучения, что уменьшает общую эффективность, как показано на рисунке 1. Одной из основных особенностей LayerNorm, которая широко рассматривается как вклад в стабилизацию, является его свойство инвариантности к повторному центрированию: суммированные входы после LayerNorm остаются неизменными, когда входы или матрица весов сдвигаются на некоторую величину шума. В подходе с RMSNorm утверждается, что эта нормализация среднего не уменьшает дисперсию скрытых состояний или градиентов модели, и предполагается, что она оказывает небольшое влияние на успех LayerNorm.
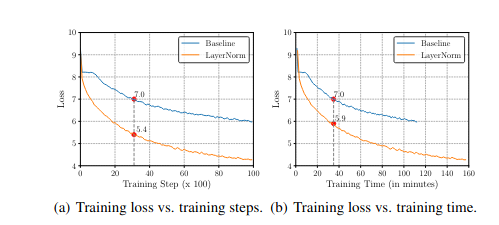
Рис.1. Процедура обучения GRU-based RNNSearch для первых 10 тыс. шагов обучения. Базовая линия означает исходную модель без какой-либо нормализации. Когда loss обучения Baseline достигает 7,0, loss с LayerNorm достигает 5,4 после того же количества шагов обучения 1(a), но только 5,9 после того же времени обучения 1(b).
В этой статье предлагается нормализацию слоя на основе среднеквадратичного значения (RMSNorm), которая регулирует суммированные входы нейрона в одном слое только с помощью статистики среднеквадратичного значения (RMS).
RMSNorm уменьшает количество вычислений и повышает эффективность по сравнению с LayerNorm. Несмотря на более простую формулировку, нормализатор RMS помогает стабилизировать величину активаций слоя, обеспечивая инвариантность к повторному масштабированию как весов, так и наборов данных. В статье также показывается возможность оценки RMS на подмножестве суммированных входов, сохраняя это свойство инвариантности. Предполагая, что суммированные входы имеют независимую одинаково распределенную структуру, предлагается частичный RMSNorm, где только первые \(p\%\) суммированных входов используются для оценки RMS.
Была проведена провека на различных задачах, включая машинный перевод, классификацию изображений, поиск подписей к изображениям и ответы на вопросы. Экспериментальные результаты показывают, что RMSNorm демонстрирует сопоставимую производительность с LayerNorm, но превосходит его по скорости выполнения с ускорением на 7%~64%. При оценке RMS с частичными (6,25%) суммированными входами, pRMSNorm достигает конкурентоспособной производительности по сравнению с RMSNorm.
Общая проблема - зачем нужны слои нормализации
Одним из узких мест, от которых, как предполагается, страдают глубокие нейронные сети, является проблема внутреннего ковариатного сдвига, при котором распределение входов слоя изменяется по мере обновления предыдущих слоев, что значительно замедляет обучение. Одно из перспективных направлений решения этой проблемы — нормализация. Иоффе и Сегеди представили пакетную нормализацию (BatchNorm) для стабилизации активаций на основе статистик среднего и дисперсии, оцениваемых из каждого обучающего мини-пакета. К сожалению, зависимость от обучающих данных лишает BatchNorm возможности обрабатывать последовательности переменной длины, хотя несколько исследователей разрабатывают различные стратегии для её применения в рекуррентных нейронных сетях (RNN). Вместо этого Салиманс и Кингма предложили нормализацию весов (WeightNorm) для перепараметризации матрицы весов, чтобы отделить длину векторов весов от их направлений. Ба и др. предложили нормализацию слоя, которая отличается от BatchNorm тем, что статистики оцениваются непосредственно из того же слоя без доступа к другим обучающим примерам. Благодаря своей простоте и эффективности, LayerNorm успешно применялась в различных глубоких нейронных моделях и достигла передовых результатов в различных задачах.
Эти исследования проложили путь для направления исследований, которое интегрирует нормализацию как часть архитектуры модели. Этот подход обеспечивает многообещающую производительность, сокращая сходимость модели, но за счет увеличения времени на каждый шаг выполнения. Для повышения эффективности Арпит и др. используют метод, независимый от данных, для приблизительной оценки статистик среднего и дисперсии, избегая тем самым вычисления пакетных статистик. Иоффе предложил повторную нормализацию пакета, чтобы уменьшить зависимость от мини-пакетов в BatchNorm. Ульянов и др. заменили пакетную нормализацию нормализацией экземпляра для генерации изображений. Хоффер и др. и У и др. обнаружили, что l1-норма может служить альтернативой дисперсии в BatchNorm с преимуществом меньшего количества нелинейных операций и более высокой вычислительной эффективности. Тем не менее, все эти работы по-прежнему следуют исходной структуре нормализации и используют статистику среднего, оцениваемую из всех суммированных входов, для обработки инвариантности к повторному центрированию.
В отличие от этих связанных работ, предложенный RMSNorm модифицирует структуру нормализации, удаляя операцию повторного центрирования и регулируя суммированные входы только с помощью RMS. Модель сохраняет лишь свойство инвариантности к повторному масштабированию, которое, как было обнаружено, может быть унаследовано, когда RMS оценивается только по подмножеству суммированных входов, частично вдохновлённая групповой нормализацией. Как побочный эффект, модель уменьшает вычислительные накладные расходы и повышает эффективность.
Недавно Чжан и др. показали, что при тщательной инициализации, residual networks могут обучаться так же стабильно, как и с нормализацией. Однако этот подход в основном направлен на улучшение residual networks и не может быть свободно переключён без модификации всех слоёв инициализации. Кроме того, его нетривиально адаптировать к другим общим нейронным сетям, таким как рекуррентные нейронные сети, где глубина модели расширяется вдоль переменной длины последовательности. В отличие от этого, предложенная модель проста, эффективна и может использоваться в качестве замены LayerNorm без дополнительных изменений.
LayerNorm
В этом разделе кратко рассмотрим LayerNorm на основе стандартной нейронной сети прямого распространения. Учитывая входной вектор \(x \in \mathbb{R}^m\), нейронная сеть прямого распространения проецирует его в выходной вектор \(y \in \mathbb{R}^n\) через линейное преобразование, за которым следует нелинейная активация, как показано ниже:
\[ a_i = \sum_{j=1}^{m} w_{ij} x_j, \quad y_i = f(a_i + b_i), \tag{1}\]
где \(w_i\) — вектор весов для \(i\)-го выходного нейрона, \(b_i\) — скаляр смещения, который обычно инициализируется нулем, а \(f(\cdot)\) — поэлементная нелинейная функция. \(a \in \mathbb{R}^n\) обозначает взвешенно-суммированные входы нейронов, которые также являются целью нормализации.
Эта базовая сеть может страдать от проблемы внутреннего ковариатного сдвига [12], где распределение входов слоя изменяется по мере обновления предыдущих слоев. Это может негативно повлиять на стабильность градиентов параметров, замедляя сходимость модели. Чтобы уменьшить этот сдвиг, LayerNorm нормализует суммированные входы, фиксируя их среднее и дисперсию следующим образом:
\[ \bar{a}_i = \frac{a_i - \mu}{\sigma} g_i, \quad y_i = f(\bar{a}_i + b_i), \tag{2}\]
где \(\bar{a}_i\) — это \(i\)-е значение вектора \(\bar{a} \in \mathbb{R}^n\), который действует как нормализованная альтернатива \(a_i\) для активации слоя. \(g \in \mathbb{R}^n\) — это параметр усиления, используемый для повторного масштабирования стандартизированных суммированных входов, и изначально устанавливается равным 1. \(\mu\) и \(\sigma^2\) — это среднее и дисперсия, соответственно оцениваемые из исходных суммированных входов \(a\):
\[ \mu = \frac{1}{n} \sum_{i=1}^{n} a_i, \quad \sigma = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (a_i - \mu)^2}. \tag{3}\]
Таким образом, LayerNorm заставляет норму нейронов быть независимой от входов и матрицы весов.
RMSNorm
Хорошо известным объяснением успеха LayerNorm является его свойство инвариантности к повторному центрированию и масштабированию. Первое позволяет модели быть нечувствительной к шумовым сдвигам как на входах, так и на весах, а второе сохраняет выходные представления неизменными, когда и входы, и веса случайно масштабируются. В этой статье выдвигается гипотеза, что инвариантность к повторному масштабированию является причиной успеха LayerNorm, а не инвариантность к повторному центрированию.
Была предложена RMSNorm, которая фокусируется только на инвариантности к повторному масштабированию и регулирует суммированные входы просто в соответствии со статистикой среднеквадратичного значения (RMS):
\[ \bar{a}_i = \frac{a_i}{\text{RMS}(a)} g_i, \quad \text{где} \quad \text{RMS}(a) = \sqrt{\frac{1}{n} \sum_{i=1}^{n} a_i^2}. \tag{4}\]
Интуитивно RMSNorm упрощает LayerNorm, полностью удаляя среднее значение в уравнении (3), жертвуя инвариантностью, которую обеспечивает нормализация среднего. Когда среднее суммированных входов равно нулю, RMSNorm точно равен LayerNorm. Хотя RMSNorm не повторно центрирует входы, он сохраняет преимущества инвариантности к масштабированию.
В таблице 1 представлены свойства инвариантности различных методов нормализации. Символ "1" указывает на инвариантность, тогда как "0" обозначает противоположное.
| Weight matrix re-scaling | Weight matrix re-centering | Weight vector re-scaling | Dataset re-scaling | Dataset re-centering | Single training case re-scaling | |
|---|---|---|---|---|---|---|
| BatchNorm | 1 | 0 | 1 | 1 | 1 | 0 |
| WeightNorm | 1 | 0 | 1 | 0 | 0 | 0 |
| LayerNorm | 1 | 1 | 0 | 1 | 0 | 1 |
| RMSNorm | 1 | 0 | 0 | 1 | 0 | 1 |
| pRMSNorm | 1 | 0 | 0 | 1 | 0 | 1 |
Таблица 1.Свойства инвариантности различных методов нормализации. «1» указывает на инвариантность, а «0» обозначает противоположность
При нормализации суммированных входов, как в LayerNorm, показано через эксперименты, что это свойство не является фундаментальным для успеха LayerNorm, и что RMSNorm является столь же или более эффективным.
RMS измеряет квадратичное среднее входов, что в RMSNorm заставляет суммированные входы попадать в \(\sqrt{n}\)-масштабированную единичную сферу. Таким образом, распределение выходов остается неизменным независимо от масштабирования распределений входов и весов, что благоприятно сказывается на стабильности активаций слоя. Хотя евклидова норма, которая отличается от RMS лишь множителем \(\sqrt{n}\), успешно исследовалась, эмпирически обнаружили, что она не работает для нормализации слоя. Предполагаем, что масштабирование сферы с размером входного вектора важно, так как это делает нормализацию более устойчивой для векторов разного размера.
Анализ инвариантности
Анализ инвариантности измеряет, насколько сильно изменяется выход модели после нормализации в соответствии с её входом и матрицей весов. Ba и др. показывают, что различные методы нормализации демонстрируют разные свойства инвариантности, что значительно способствует устойчивости модели. В этом разделе мы теоретически исследуем свойства инвариантности RMSNorm.
Рассмотрим следующую общую форму RMSNorm:
\[ y = f\left(\frac{Wx}{\text{RMS}(a)} \cdot g + b\right), \tag{5}\]
где \(\cdot\) обозначает поэлементное умножение. Основные результаты суммированы в таблице 1. RMSNorm инвариантен как к матрице весов, так и к повторному масштабированию входа благодаря следующему линейному свойству RMS:
\[ \text{RMS}(\alpha x) = \alpha \text{RMS}(x), \tag{6}\]
где \(\alpha\) — значение масштаба. Предположим, что матрица весов масштабируется на коэффициент \(\delta\), то есть \(W' = \delta W\), тогда это изменение не влияет на окончательный выход слоя:
\[ y' = f\left(\frac{W'x}{\text{RMS}(a')} \cdot g + b\right) = f\left(\frac{\delta Wx}{\delta \text{RMS}(a)} \cdot g + b\right) = y. \tag{7}\]
Напротив, если масштабирование выполняется только на отдельных векторов весов, это свойство больше не сохраняется, так как различные коэффициенты масштабирования нарушают линейное свойство RMS. Аналогично, если мы применим масштаб к входу с коэффициентом \(\delta\), то есть \(x' = \delta x\), выход RMSNorm остается неизменным через анализ, аналогичный уравнению 7. Мы можем легко расширить это равенство на пакетные входы, а также на весь набор данных. Следовательно, RMSNorm инвариантен к масштабированию своих входов.
Основное отличие от LayerNorm заключается в том, что RMSNorm не повторно центрируется и, таким образом, не демонстрирует аналогичного линейного свойства для переменного сдвига. Он не инвариантен ко всем операциям повторного центрирования.
Анализ градиента
Приведенный выше анализ рассматривает только эффект масштабирования входов и матрицы весов на выход слоя. Однако в общем случае нейронная сеть, усиленная RMSNorm, обучается с помощью стандартного подхода стохастического градиентного спуска, где устойчивость градиента модели очень важна для обновления параметров и сходимости модели (см. также Santurkar и др. [23], которые утверждают, что успех методов нормализации обусловлен не добавленной стабильностью к входам слоя, а увеличением гладкости оптимизации).
При заданной функции потерь \(L\) мы выполняем обратное распространение через уравнение (4) для получения градиента относительно параметров \(g\) и \(b\) следующим образом:
\[ \frac{\partial L}{\partial b} = \frac{\partial L}{\partial v}, \quad \frac{\partial L}{\partial g} = \frac{\partial L}{\partial v} \cdot \frac{Wx}{\text{RMS}(a)}, \tag{8}\]
где \(v\) — сокращение для всего выражения внутри \(f(\cdot)\) в уравнении (4), а \(\frac{\partial L}{\partial v}\) — градиент, обратно распространяемый от \(L\) к \(v\). Оба градиента \(\frac{\partial L}{\partial b}\) и \(\frac{\partial L}{\partial g}\) инвариантны к масштабированию входов \(x\) и матрицы весов \(W\) (в случае \(\frac{\partial L}{\partial g}\) благодаря линейному свойству в уравнении (6)). Кроме того, градиент \(g\) пропорционален нормализованным суммированным входам, а не исходным входам. Это обеспечивает стабильность величины \(g\).
В отличие от этих векторных параметров, градиент матрицы весов \(W\) более сложен из-за квадратичных вычислений в RMS. Формально:
\[ \frac{\partial L}{\partial W} = \sum_{i=1}^{n} \left[ x^T \otimes \left( \text{diag}\left( g \frac{\partial L}{\partial v} \right) \times R \right) \right]_i,\]
где
\[ R = \frac{1}{\text{RMS}(a)} \left( I - \frac{(Wx)(Wx)^T}{n \text{RMS}(a)^2} \right), \tag{9}\]
\(\text{diag}(\cdot)\) обозначает диагональную матрицу входа, \(\otimes\) обозначает произведение Кронекера, а \(I\) — единичную матрицу. Для ясности мы явно используем \(\times\) для обозначения матричного умножения. Матричный член \(R\) связывает градиент \(W\) как с входами \(x\), так и с матрицей весов \(W\). С помощью тщательного анализа мы можем продемонстрировать, что этот член отрицательно коррелирует как с масштабированием входа, так и с масштабированием матрицы весов.
После применения масштаба \(\delta\) либо к входу \(x\) (\(x' = \delta x\)), либо к матрице весов (\(W' = \delta W\)), мы имеем:
\[ R' = \frac{1}{\delta \text{RMS}(a)} \left( I - \frac{(\delta Wx)(\delta Wx)^T}{n \delta^2 \text{RMS}(a)^2} \right) = \frac{1}{\delta} R. \tag{10}\]
Если мы подставим масштабированный член \(R'\) обратно в уравнение (9), мы можем легко доказать, что градиент \(\frac{\partial L}{\partial W}\) инвариантен к масштабированию входа, но сохраняет отрицательную корреляцию с масштабированием матрицы весов. Уменьшение чувствительности градиента \(\frac{\partial L}{\partial W}\) к масштабированию входов обеспечивает его гладкость и улучшает стабильность обучения. С другой стороны, отрицательная корреляция действует как неявный адаптер скорости обучения и динамически контролирует норму градиентов, что избегает матрицы весов с большой нормой и улучшает сходимость модели.
pRMSNorm
Свойство инвариантности к масштабированию RMSNorm приписывается линейному свойству RMS. Учитывая, что нейроны в одном слое часто имеют независимую одинаково распределенную структуру, мы утверждаем, что RMS может быть оценен на подмножестве этих нейронов, а не на всех. Мы предлагаем частичный RMSNorm (pRMSNorm). При заданном ненормализованном входе \(a\), pRMSNorm выводит статистику RMS из первых \(p\%\) элементов \(a\):
\[ \text{RMS}(a) = \sqrt{\frac{1}{k} \sum_{i=1}^{k} a_i^2}, \]
где \(k = n \cdot p\) обозначает количество элементов, используемых для оценки RMS. Линейное свойство все еще сохраняется для RMS, как в уравнении (6), что указывает на то, что pRMSNorm обладает теми же свойствами инвариантности, что и RMSNorm, как показано в таблице 1.
RMS является смещенной оценкой RMS, которая часто бывает неточной. Хотя теоретически pRMSNorm приближается к RMSNorm, мы наблюдаем нестабильность градиента, где градиент склонен к взрыву при малом \(m\). Однако на практике модели с pRMSNorm могут успешно достигать удовлетворительной сходимости с частичным соотношением 6,25%.
Эксперименты
Чтобы протестировать эффективность нормализации слоя в различных реализациях, исследователи провели эксперименты с использованием TensorFlow, PyTorch и Theano. Они добавляли RMSNorm к различным моделям, сравнивая их с ненормализованным базовым вариантом и LayerNorm. Эти модели основаны на различных архитектурах, охватывающих различные варианты RNN, сверточные и self-attention модели, а также различные активации (такие как сигмоида, tanh и softmax), с инициализацией, варьирующейся от равномерной, нормальной, ортогональной с различными диапазонами инициализации или дисперсией. Если не указано иное, все статистики, связанные со скоростью, измеряются на одной TITAN X (Pascal). Сообщаемое время усредняется по трем запускам.
На рисунке 2 представлен SacreBLEU score на newstest2013 для RNNSearch. Модели реализованы в соответствии с Nematus [25] в TensorFlow.
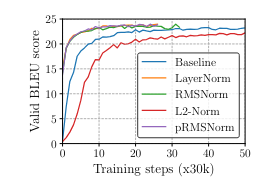
Рис.2. Оценка SacreBLEU на newstest2013 для RNNSearch.
| Model | Test14 | Test17 | Time |
|---|---|---|---|
| Baseline | 21.7 | 23.4 | 399±3.40s |
| LayerNorm | 22.6 | 23.6 | 665±32.5s |
| L2-Norm | 20.7 | 22.0 | 482±19.7s |
| RMSNorm | 22.4 | 23.7 | 501±11.8s (24.7%) |
| pRMSNorm | 22.6 | 23.1 | 493±10.7s (25.9%) |
В таблице 2 представлен SacreBLEU score на newstest2014 (Test14) и newstest2017 (Test17) для RNNSearch с использованием TensorFlow-версии Nematus. "Time" — время в секундах на 1k шагов обучения. Мы установили \(p\) равным 6.25%. Мы выделяем лучшие результаты жирным шрифтом и показываем ускорение RMSNorm по сравнению с LayerNorm в скобках.
Информацию об экспериментах вы можете посмотреть в оригинальной статье.
