Разбираемся с Rotary Positional Encoding - вращательным позиционным кодированием

Rotary Positional Embeddings — это современная техника позиционного кодирования для обработки естественного языка (NLP). Многие популярные большие языковые модели, такие как Llama, Llama2, PaLM и CodeGen, уже используют её вместо абсолютных эмбеддингов, которые использовались в оригинальной статье "Attention is all you need", или относительного позиционного кодирования, предложенного в статье "Self-Attention with Relative Position Representations".

До появления Rotary Positional Embedding не было однозначного ответа на вопрос, что лучше — абсолютное или относительное позиционное кодирование. Однако, как всегда, при сравнении двух техник ответ заключается в их комбинации, что и даёт нам Rotary Positional Embedding.

Тут мы обсудим:

1. Основной недостаток абсолютного позиционного кодирования
2. Основные недостатки относительного позиционного кодирования
3. Что такое Rotary Positional Encoding и как оно работает
4. Как Rotary Positional Encoding преодолевает недостатки абсолютного и относительного позиционного кодирования

Для начала:

Мы знаем, что нам нужно позиционное кодирование, потому что self-attention не учитывает позицию слова в последовательности.

Абсолютное позиционное кодирование — это форма позиционного кодирования, где мы используем синусоидальные функции для создания позиционного эмбеддинга (t, d), где каждый элемент (d,) соответствует позиции (pos1, pos2, ..., pos_T). Абсолютные позиционные кодировки добавляются поэлементно к входным эмбеддингам токеннов.

Относительное позиционное кодирование — это форма позиционного кодирования, где мы используем парные расстояния между одной позицией и другими позициями. Относительные позиционные кодировки добавляются поэлементно к матрице внимания формы (B, T, T) перед слоем Softmax.

Основной недостаток абсолютного позиционного кодирования

• Не включает относительную позиционную информацию

Хотя абсолютное позиционное кодирование захватывает позиционную информацию для слова, оно не захватывает позиционную информацию для всего предложения (или последовательности!).

Пример:

Общий способ создания абсолютного позиционного кодирования длиной 3 — это случайная инициализация.

→ Предположим, мы получаем следующее: [0.1, 0.01, 0.5]. (Это абсолютное позиционное кодирование обеспечит, чтобы одинаковые слова в разных позициях имели разные выходы внимания) Однако обратите внимание, что происходит, если мы проанализируем абсолютное позиционное кодирование: [0.1, 0.01, 0.05]:

(1) Нет отношений между позициями.

• Позиционное кодирование на больших индексах позиций может быть больше или меньше, чем на меньших индексах позиций.
• Позиционное кодирование на позиции 1 (0.1) может быть больше, чем позиционное кодирование на позиции 2 (0.01), т.е. [0.1 > 0.01].
• Позиционное кодирование на позиции 1 (0.1) также может быть меньше, чем позиционное кодирование на позиции 3 (0.5), т.е. [0.1 < 0.5].

(2) Относительные расстояния непостоянны.

• Различия в позиционном кодировании не говорят нам, насколько далеко друг от друга находятся слова.
• Расстояние от позиции 1 до позиции 2 равно abs(0.1-0.01) = 0.09.
• Расстояние от позиции 1 до позиции 3 равно abs(0.1-0.05) = 0.05. (Идеально расстояние от позиции 1 до позиции 3 должно быть больше, чем расстояние от позиции 1 до позиции 2) Это означает, что абсолютное позиционное кодирование не захватывает позиционную информацию для всего предложения (или последовательности!).

Основные недостатки относительного позиционного кодирования

1. Вычислительно неэффективно:

Необходимо создать дополнительный шаг для само-внимания позже.

• Помните, что нам пришлось создать матрицу парного позиционного кодирования, а затем выполнить довольно много манипуляций с тензорами, чтобы получить относительные позиционные кодировки на каждом временном шаге.

2. Не подходит для инференса

Во время инференса для ускорения работы хочется использовать метод, называемый KV cache, который помогает увеличить скорость вычислений.

Одно из требований для использования KV cache заключается в том, чтобы позиционное кодирование для слов, которые уже были сгенерированы, не изменялось при генерации новых слов (что обеспечивает абсолютное позиционное кодирование).

Относительные позиционные кодировки поэтому не подходят для KV-cache, потому что вложения для каждого токена изменяются на каждом новом временном шаге.

Пример:

Когда ваша последовательность имеет длину 2, относительные позиции для слова будут [-1, 0, 1]. Когда ваша входная последовательность имеет длину 3, относительные позиции для слова будут [-2, -1, 0, 1, 2]. Поскольку мы используем эти относительные позиции для получения относительных позиционных кодировок для каждого слова, когда набор относительных позиций изменяется, ваши позиционные кодировки для каждого слова изменяются.

Это означает, что для предложения ['это', 'супер', 'круто'], ваше позиционное кодирование слова 'это' изменяется на каждом временном шаге, когда вы генерируете токены для вывода.

Поэтому относительное позиционное кодирование сейчас почти не используется.

Что такое Rotary Positional Encoding

Rotary Positional Encoding — это тип позиционного кодирования, который кодирует абсолютную позиционную информацию с помощью матрицы вращения и естественным образом включает явную зависимость относительной позиции в формулировку само-внимания.

Что такое матрица вращения?

Как следует из её названия, матрица вращения — это матрица, которая вращает вектор в другой вектор на некоторый угол. Матрица вращения выводится из тригонометрических свойств синуса и косинуса, которые мы изучали в школе, и должно быть достаточно интуитивно понятной матрицы вращения, используя двумерную, как показано ниже! (См. ссылку ниже для вывода двумерной матрицы вращения, если вы не уверены).

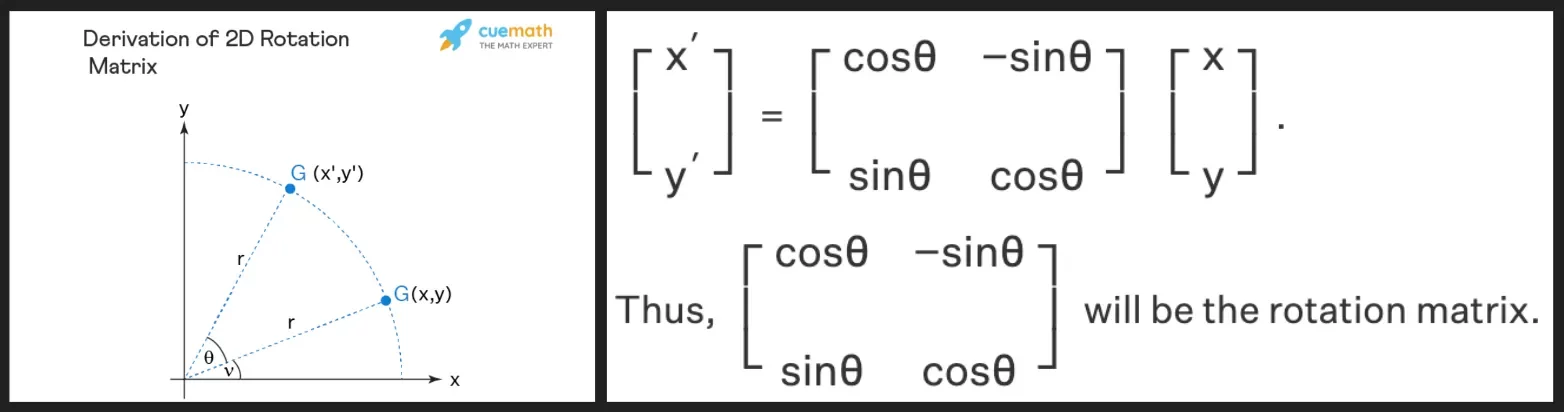
Рис.1. Двумерное вращение

Мы видим, что матрица вращения сохраняет величину (или длину) исходного вектора \(r\), как видно на изображении выше, и единственное, что изменяется, — это угол к оси x.

Как двумерная матрица вращения участвует в Rotary Positional Encoding?

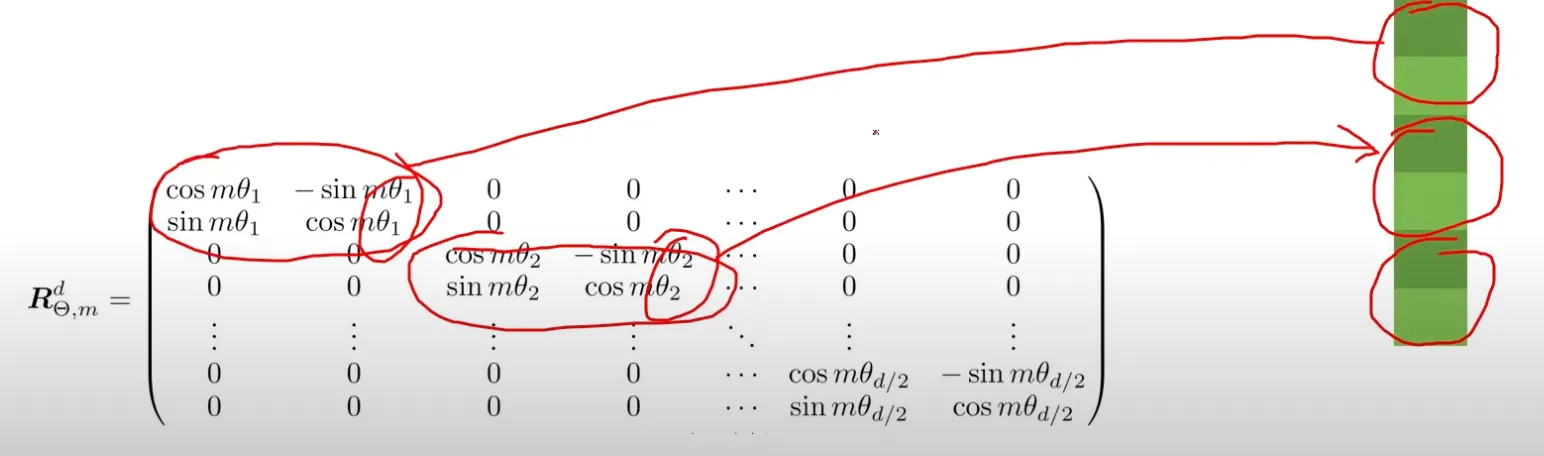
Рис.2. Применяем двумерное вращение к компнентам эмбеддинга токена

• Матрицы вращения, используемые в Rotary Positional Encoding, представляют собой несколько блоков двумерной матрицы вращения, как показано выше!
• И если взять вектор (эмбеддинг токена) и умножить его на пресдтавленную матрицу - то это и есть RoPE преобразование.
• Весь фокус только в том как задать углы θ(m,i) для каждой позиции и компоненты эмбединга токена.

Формула вычисления углов для Rotary Positional Embedding (RoPE) зависит от номера позиции m и пары размерностей эмбеддинга. Для каждой пары размерностей i угол \(θ(m,i)\) рассчитывается как:

\[ \begin{align} θ(m,i)=m⋅θ_i​ \\ θ_i​= 10000^{-2(i-1) / d} \\ i = 1, 2, \ldots, \frac{d}{2} \\ \end{align}\]

Здесь:

• \(m\) — номер позиции токена в последовательности,
• \(i\) — индекс пары размерностей эмбеддинга (начиная с 1),
• \(d\) — общая размерность эмбеддинга,
• \(θ_i \) — базовая частота для пары размерностей, определяемая через фиксированное основание 10000

Эта формула гарантирует, что углы вращения зависят от относительного положения токенов и уникальны для каждой пары размерностей.

Гиперпараметры d и 10000 (base) задаются заранее и не изменяются в процессе обучения.

Первый вопрос, который возникает когда это видишь: "Почему?"

Поскольку наши векторы имеют гораздо более двух измерений, и легко понять двумерную матрицу вращения, авторы придумали умный способ использовать двумерную матрицу вращения для вращения всего d-мерного вектора.

Идея заключается в использовании различных двумерных матриц вращения для каждой пары измерений (каждый набор векторов размером 2) на некоторый угол. Поскольку мы используем "пары измерений", нам потребуется, чтобы \(d\) делилось на 2, что не проблема, все размерности моделей четны.

Пример:

Дано предложение [this, is, awesome], давайте посмотрим, как оно вращает позиционное кодирование для слов 'this' и 'is'. Предположим, что вложения для слов являются шестимерными векторами:

• 'this': [x1, x2, x3, x4, x5, x6].
• 'is': [x7, x8, x9, x10, x11, x12].

Мы знаем, что:

• Слово 'this' находится на позиции 0, поэтому m = 0. (Обратите внимание, что это будет одинаково для всех матриц вращения для слова 'this')
• Слово 'is' находится на позиции 1, поэтому m = 1. (Обратите внимание, что это будет одинаково для всех матриц вращения для слова 'is') Поскольку у нас есть шестимерные векторы, это означает, что у нас есть (6/2) = 3 пары двумерных векторов для каждого слова (также 3 матрицы вращения).

Для каждого слова, поскольку у нас есть 3 пары двумерных векторов, у нас будет 3 разных θ, которые разделяются между словами 'this' и 'is'.

• Давайте предположим, что θ равна [0.1, 0.4, 0.6].

Поскольку у нас есть 3 пары двумерных векторов (в наших примерах вложения являются шестимерными векторами), у нас будет: (1) 3 матрицы вращения для каждого слова, и, следовательно, (2) 3 угла для каждого слова (рассчитанные как \(m * θ_i\)) для вращения.

• 3 угла для 'this': \([m=0 * {\theta}_0=0.1, m=0 * {\theta}_1=0.4, m=0 * {\theta}_2=0.6] = [0, 0, 0]\).
• 3 угла для 'is': \([m=1 * \theta_0=0.1, m=1 * \theta_1=0.4, m=1 * \theta_2=0.6] = [0.1, 0.4, 0.6]\).

Если мы подставим эти значения в матрицу вращения выше и умножим наш шестимерный вектор для слова 'this':

• Мы вращаем [x1, x2] на угол 0.
• Мы вращаем [x3, x4] на угол 0.
• Мы вращаем [x5, x6] на угол 0.

Если мы подставим эти значения в матрицу вращения выше и умножим наш шестимерный вектор для слова 'is':

• Мы вращаем [x7, x8] на угол 0.1.
• Мы вращаем [x9, x10] на угол 0.4.
• Мы вращаем [x11, x12] на угол 0.6.

Это означает, что каждый эмбеддинг токена вращается тремя парами матриц вращения, каждая с различными вращениями, которые зависят от позиций каждого токена.

Это означает, что позиционное кодирование будет учитывать позицию слова, и теперь мы сможем генерировать разные выходы внимания для одного и того же слова в разных позициях.

Как Rotary Positional Encoding преодолевает недостатки абсолютного и относительного позиционного кодирования

Rotary Positional Encoding преодолевает недостатки, комбинируя два подхода - абсолютного и относительного позиционного кодирования.

Абсолютное позиционное кодирование в Rotary Positional Encoding

Обратите внимание в нашем примере для Rotary Positional Encoding для 'this' и 'is', что матрица вращения зависит только от \(m * \theta_i\), где \(\theta_i\) разделяется между всеми словами, а \(m\) — это просто позиция слова (без учета позиций других слов). Подобно абсолютному позиционному кодированию, у нас есть одно позиционное кодирование для одной позиции (не зависящее от позиций других слов).

Относительное позиционное кодирование в Rotary Positional Encoding

Поскольку угол вращения зависит от \(m * \theta_i\), слова в начале предложения будут иметь меньший угол вращения, а слова, достигающие конца предложения, будут иметь больший угол вращения, делая расстояния относительными.

• Помните: \(\theta_i\) одинаково для всех слов, \(m\) — позиция слова — это единственное, что изменяется. Большее m означает \(m * \theta_i\), что означает больший угол вращения.

Подобно относительному позиционному кодированию, существует связь между позиционными кодировками разных позиций.

Теперь, чтобы объяснить, почему оно преодолевает недостатки, давайте рассмотрим недостатки обоих методов:

Абсолютное позиционное кодирование:

• (1) Не включает относительную позиционную информацию.

Относительное позиционное кодирование:

• (2) Вычислительно неэффективно,
• (3) Не подходит для вывода.

Поэтому мы знаем, что Rotary Positional Encoding должно иметь следующие свойства:

• Включает относительную позиционную информацию.
• Быть вычислительно эффективным.
• Быть подходящим для инференса.

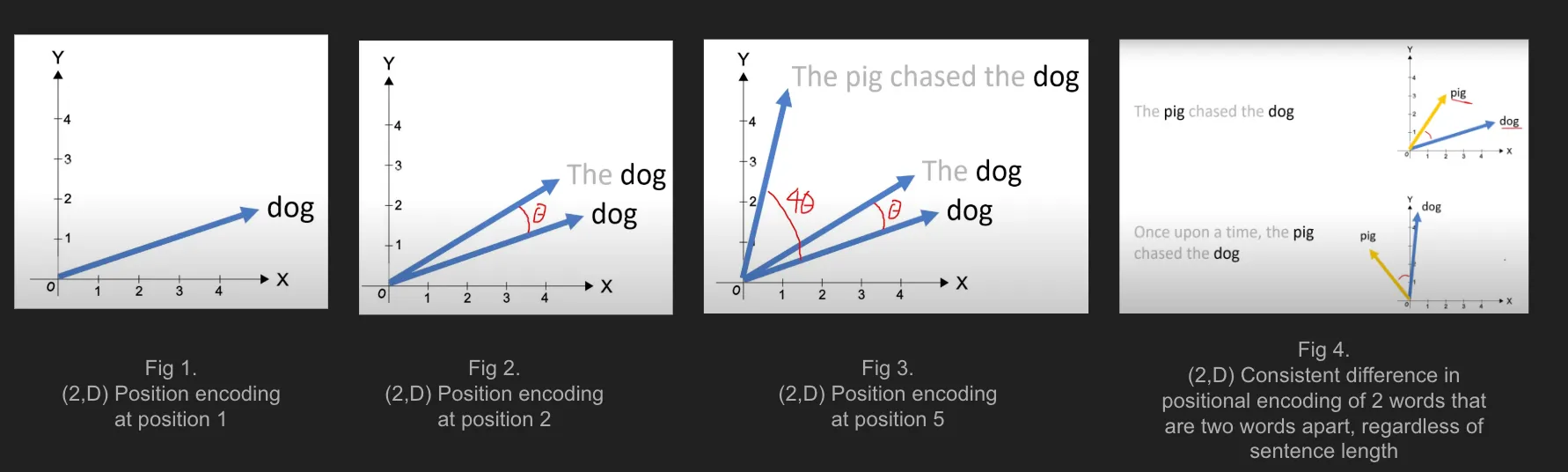
Рис.3. Rotary Positional Encoding включает относительную позиционную информацию

(Свойство 1) Rotary Positional Encoding включает относительную позиционную информацию

Rotary Positional Encoding включает относительную позиционную информацию, делая углы в матрице вращения зависимыми от текущей позиции слова, и благодаря свойствам матрицы вращения, говорит нам, насколько далеко друг от друга находятся два слова. Например, на рис. 3 выше, угол между 'свиньей' и 'собакой' одинаков, даже если они (1) появляются в двух предложениях разной длины, и (2) 'свинья' и 'собака' появляются в разных позициях предложения!

• (если вы вычислите скалярное произведение между 'свиньей' и 'собакой' в обоих предложениях, они будут одинаковыми).
• Угол одинаков, слова 'свинья' и 'собака' всегда находятся на расстоянии двух слов друг от друга (с 'погналась за' между 'свиньей' и 'собакой').
• Помните, что угол вращения слова — это \(m * \theta_i\), а угол между 'свиньей' и 'собакой', которые находятся на расстоянии двух слов, равен \((m_{собака} - m_{свинья} = 2 * \theta_i)\).

Другой способ взглянуть на это — построить график угла внутри матрицы вращения для разных позиций:

Помните, что угол внутри матрицы вращения обозначается как: \(m * \theta_i\)

• Ось Y представляет угол вращения.
• Ось X представляет скрытое измерение.

Для графика ниже вы должны смотреть на восходящий сдвиг всего графика, чтобы исследовать влияние изменения m (позиции слова).

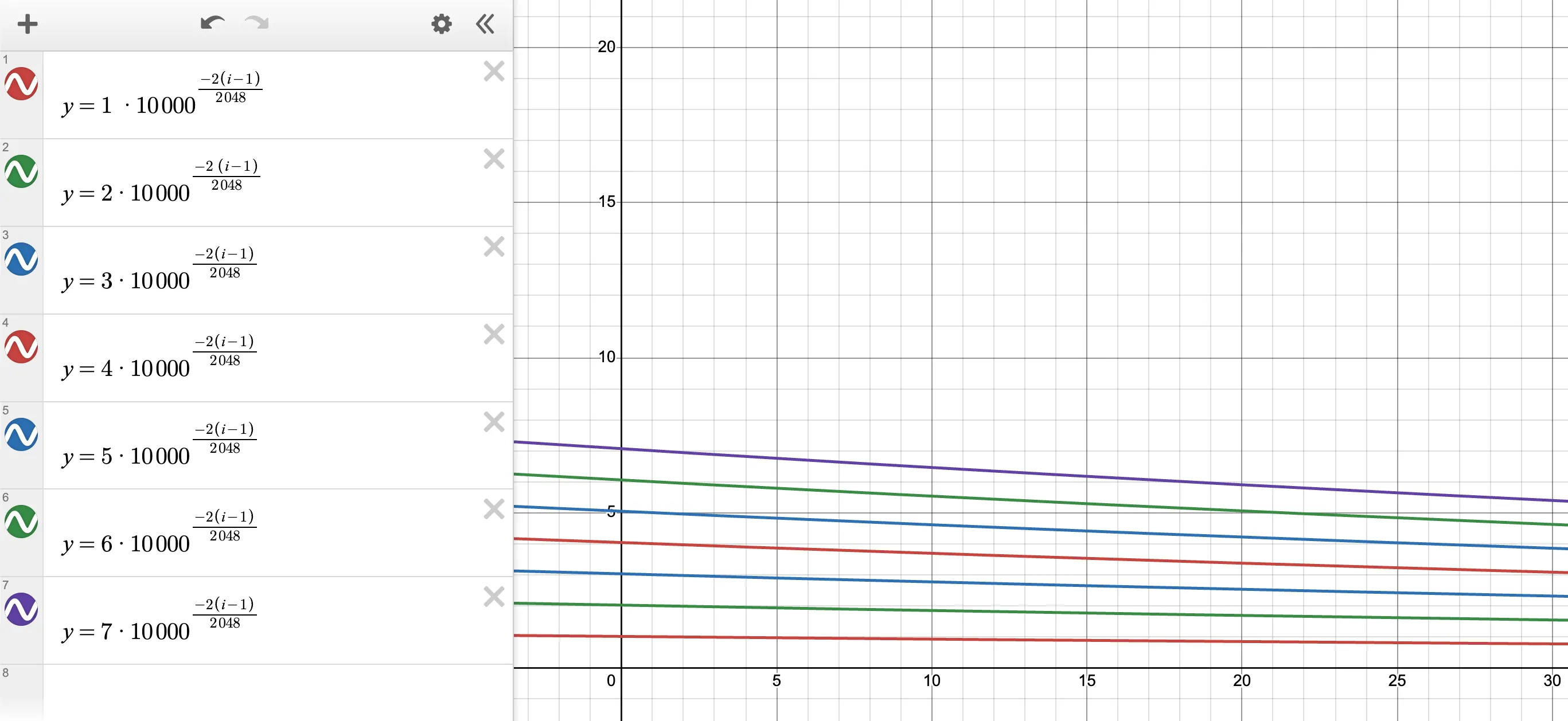
Рис.4. График углов внутри матрицы вращения для разных позиций от pos-1 до pos-7.

Из графика мы видим последовательный шаблон: когда t увеличивается от 1 до 7, угол вращения также увеличивается (как показано сдвигом всего графика). Это означает, что если позиционное кодирование слова имеет больший угол вращения, слово находится дальше в предложении. → Разрыв между t=1 и t=3 больше, чем разрыв между t=1 и t=2.

Из графика мы замечаем, что величина различий между двумя последовательными парами позиций одинакова. → Это означает, что изменение на одном временном шаге вызвало примерно такое же изменение угла вращения. Например, разрывы между t=1 и t=2 такие же, как между t=2 и t=3, и так далее. → Это означает, что относительные расстояния согласованы. Например, любые два слова, находящиеся на расстоянии трех слов друг от друга, будут иметь одинаковый угол вращения.

Другая перспектива для свойства 1 RoPE

До сих пор мы говорили только об "угле вращения", но где та часть, которая кодирует относительные расстояния от одного слова до других позиций? Ответ кроется в следующем определении скалярного произведения:

• "Скалярное произведение векторов A и B равно длине A, умноженной на длину B, умноженной на косинус угла между ними A · B = |A||B| cos(θ)".

Если мы вычислим скалярное произведение между позиционным кодированием вращения позиции 1 и другими позициями, мы получим cos(θ), который зависит только от угла вращения (более явно от разницы в угле вращения от позиции 1 до позиции другого слова).

Угол вращения для позиции = 1 меньше углов вращения для позиций > 1. Это означает, что чем дальше другое слово от позиции 1, (1) тем больше разница в угле вращения, (2) тем меньше скалярное произведение (потому что значение косинуса падает от 0 до \(\pi\)), (3) тем дальше другое слово от позиции 1.

Мы приходим к выводу, что позиционное кодирование вращения включает относительную позиционную информацию.

Как использовать Rotary Positional Encoding:

• Поскольку нам нужно, чтобы скалярное произведение включало относительное позиционное кодирование, мы применяем позиционное кодирование вращения к запросу и ключу отдельно, чтобы при их матричном умножении матрица внимания содержала относительную позиционную информацию.

Пример реализации на RoPE на pytorch https://github.com/lucidrains/rotary-embedding-torch/blob/main/rotary_embedding_torch/rotary_embedding_torch.py

(Sвойство 2) Rotary Positional Encoding вычислительно эффективно

Может показаться, что использование Rotary Positional Encoding не является вычислительно эффективным, потому что нам нужно создать матрицу вращения, но исследователи нашли вычислительно эффективную формулу.

Рис.5. Rotary Positional Embeddings (RoPE)

(Sвойство 3) Rotary Positional Encoding подходит для инференса

Поскольку мы уже знаем, что Rotary Positional Encoding похоже на абсолютное позиционное кодирование в том, что кодировки зависят только от текущей позиции слова, позиционные кодировки для слов, которые уже были сгенерированы, не изменяются, что снова делает возможным использование KV cache во время вывода.

Итого:

• Недостаток абсолютного позиционного кодирования заключается в том, что оно не учитывает относительную позиционную информацию в предложении.
• Недостаток относительного позиционного кодирования заключается в том, что оно вычислительно затратно и не подходит для вывода.
• Rotary Positional Encoding объединяет два подхода, используя преимущества каждого метода, и также использует вычислительно эффективный способ для его эффективного вычисления.
• Основная идея Rotary Positional Encoding заключается в использовании \(d/2\) двумерных матриц вращения для вращения d-мерной матрицы, где угол вращения каждой двумерной матрицы вращения определяется как \(m * \theta\) (где m — позиция слова, а \(\theta\) — предварительно вычисленный член, который разделяется между всеми словами), и создаёт экспоненциально выглядящую кривую. Когда m увеличивается, экспоненциально выглядящая кривая сдвигается вверх к большему значению, указывая на большее позиционное расстояние.